Pearson and Lee's data on the Heights of Parents and Children by Gender
Source:R/data-concepts.R
PearsonLee.RdWachsmuth et. al (2003) noticed that a loess smooth through Galton's data on heights of mid-parents and their offspring exhibited a slightly non-linear trend, and asked whether this might be due to Galton having pooled the heights of fathers and mothers and sons and daughters in constructing his tables and graphs.
To answer this question, they used analogous data from English families at about the same time, tabulated by Karl Pearson and Alice Lee (1896, 1903), but where the heights of parents and children were each classified by gender of the parent.
Format
A frequency data frame with 746 observations on the following 6 variables.
childchild height in inches, a numeric vector
parentparent height in inches, a numeric vector
frequencya numeric vector
gpa factor with levels
fdfsmdmspara factor with levels
FatherMotherchla factor with levels
DaughterSon
Source
Pearson, K. and Lee, A. (1896). Mathematical contributions to the theory of evolution. On telegony in man, etc. Proceedings of the Royal Society of London, 60 , 273-283.
Pearson, K. and Lee, A. (1903). On the laws of inheritance in man: I. Inheritance of physical characters. Biometrika, 2(4), 357-462. (Tables XXII, p. 415; XXV, p. 417; XXVIII, p. 419 and XXXI, p. 421.)
Details
The variables gp, par and chl are provided to allow
stratifying the data according to the gender of the father/mother and
son/daughter.
References
Wachsmuth, A.W., Wilkinson L., Dallal G.E. (2003). Galton's bend: A previously undiscovered nonlinearity in Galton's family stature regression data. The American Statistician, 57, 190-192. %http://staff.ustc.edu.cn/~zwp/teach/Reg/galton.pdf doi:10.1198/0003130031874 .
See the example by John Russell for the 30DayChartChallenge
Examples
data(PearsonLee)
str(PearsonLee)
#> 'data.frame': 746 obs. of 6 variables:
#> $ child : num 59.5 59.5 59.5 60.5 60.5 61.5 61.5 61.5 61.5 61.5 ...
#> $ parent : num 62.5 63.5 64.5 62.5 66.5 59.5 60.5 62.5 63.5 64.5 ...
#> $ frequency: num 0.5 0.5 1 0.5 1 0.25 0.25 0.5 1 0.25 ...
#> $ gp : Factor w/ 4 levels "fd","fs","md",..: 2 2 2 2 2 2 2 2 2 2 ...
#> $ par : Factor w/ 2 levels "Father","Mother": 1 1 1 1 1 1 1 1 1 1 ...
#> $ chl : Factor w/ 2 levels "Daughter","Son": 2 2 2 2 2 2 2 2 2 2 ...
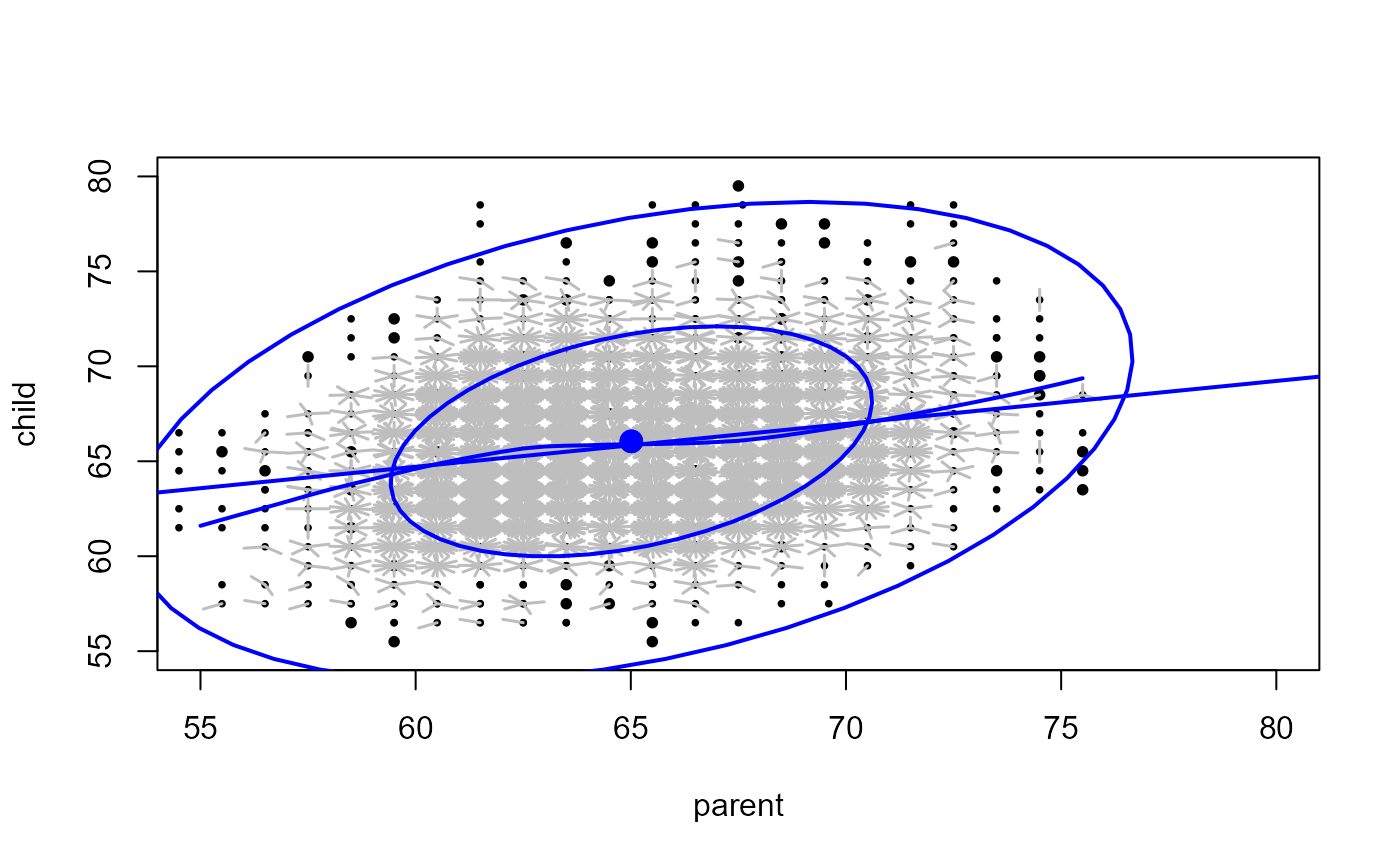
with(PearsonLee,
{
lim <- c(55,80)
xv <- seq(55,80, .5)
sunflowerplot(parent,child, number=frequency, xlim=lim, ylim=lim, seg.col="gray", size=.1)
abline(lm(child ~ parent, weights=frequency), col="blue", lwd=2)
lines(xv, predict(loess(child ~ parent, weights=frequency), data.frame(parent=xv)),
col="blue", lwd=2)
# NB: dataEllipse doesn't take frequency into account
if(require(car)) {
dataEllipse(parent,child, xlim=lim, ylim=lim, plot.points=FALSE)
}
})
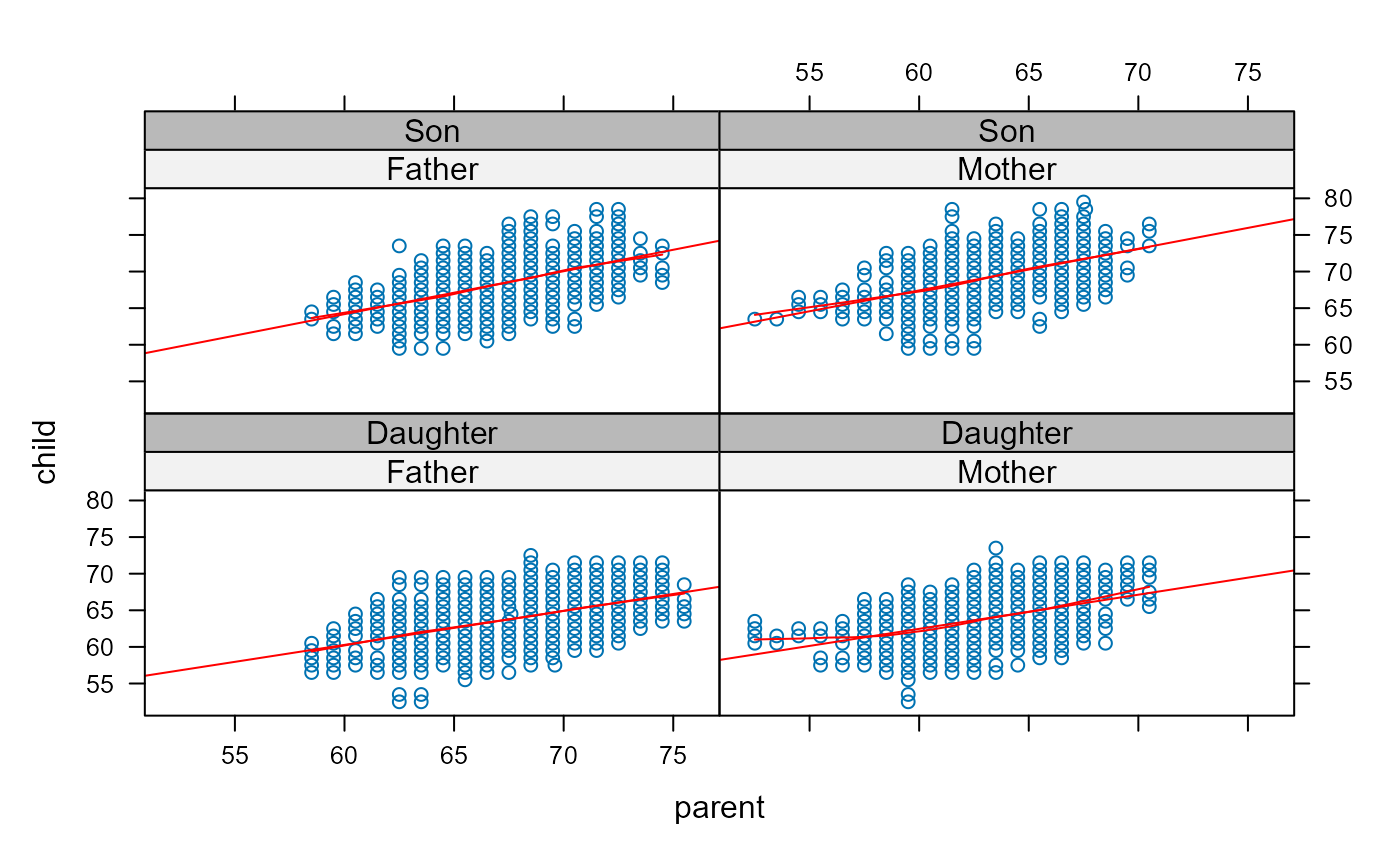
 ## separate plots for combinations of (chl, par)
# this doesn't quite work, because xyplot can't handle weights
require(lattice)
xyplot(child ~ parent|par+chl, data=PearsonLee, type=c("p", "r", "smooth"), col.line="red")
## separate plots for combinations of (chl, par)
# this doesn't quite work, because xyplot can't handle weights
require(lattice)
xyplot(child ~ parent|par+chl, data=PearsonLee, type=c("p", "r", "smooth"), col.line="red")
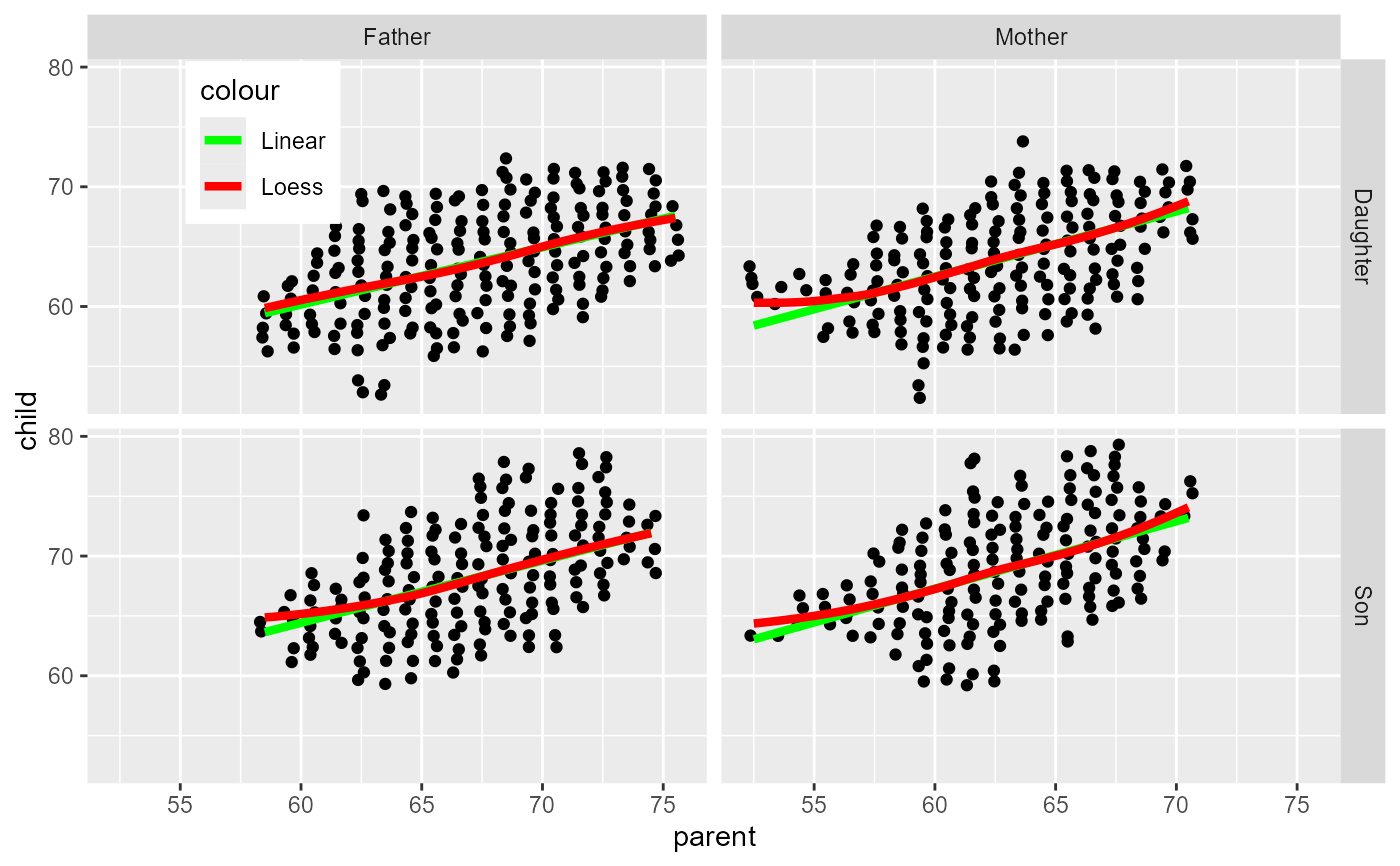
 # Using ggplot [thx: Dennis Murphy]
require(ggplot2)
ggplot(PearsonLee, aes(x = parent, y = child, weight=frequency)) +
geom_point(size = 1.5, position = position_jitter(width = 0.2)) +
geom_smooth(method = lm, aes(weight = PearsonLee$frequency,
colour = 'Linear'), se = FALSE, size = 1.5) +
geom_smooth(aes(weight = PearsonLee$frequency,
colour = 'Loess'), se = FALSE, size = 1.5) +
facet_grid(chl ~ par) +
scale_colour_manual(breaks = c('Linear', 'Loess'),
values = c('green', 'red')) +
theme(legend.position = c(0.14, 0.885),
legend.background = element_rect(fill = 'white'))
#> Warning: Use of `PearsonLee$frequency` is discouraged.
#> ℹ Use `frequency` instead.
#> Warning: Use of `PearsonLee$frequency` is discouraged.
#> ℹ Use `frequency` instead.
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
# Using ggplot [thx: Dennis Murphy]
require(ggplot2)
ggplot(PearsonLee, aes(x = parent, y = child, weight=frequency)) +
geom_point(size = 1.5, position = position_jitter(width = 0.2)) +
geom_smooth(method = lm, aes(weight = PearsonLee$frequency,
colour = 'Linear'), se = FALSE, size = 1.5) +
geom_smooth(aes(weight = PearsonLee$frequency,
colour = 'Loess'), se = FALSE, size = 1.5) +
facet_grid(chl ~ par) +
scale_colour_manual(breaks = c('Linear', 'Loess'),
values = c('green', 'red')) +
theme(legend.position = c(0.14, 0.885),
legend.background = element_rect(fill = 'white'))
#> Warning: Use of `PearsonLee$frequency` is discouraged.
#> ℹ Use `frequency` instead.
#> Warning: Use of `PearsonLee$frequency` is discouraged.
#> ℹ Use `frequency` instead.
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
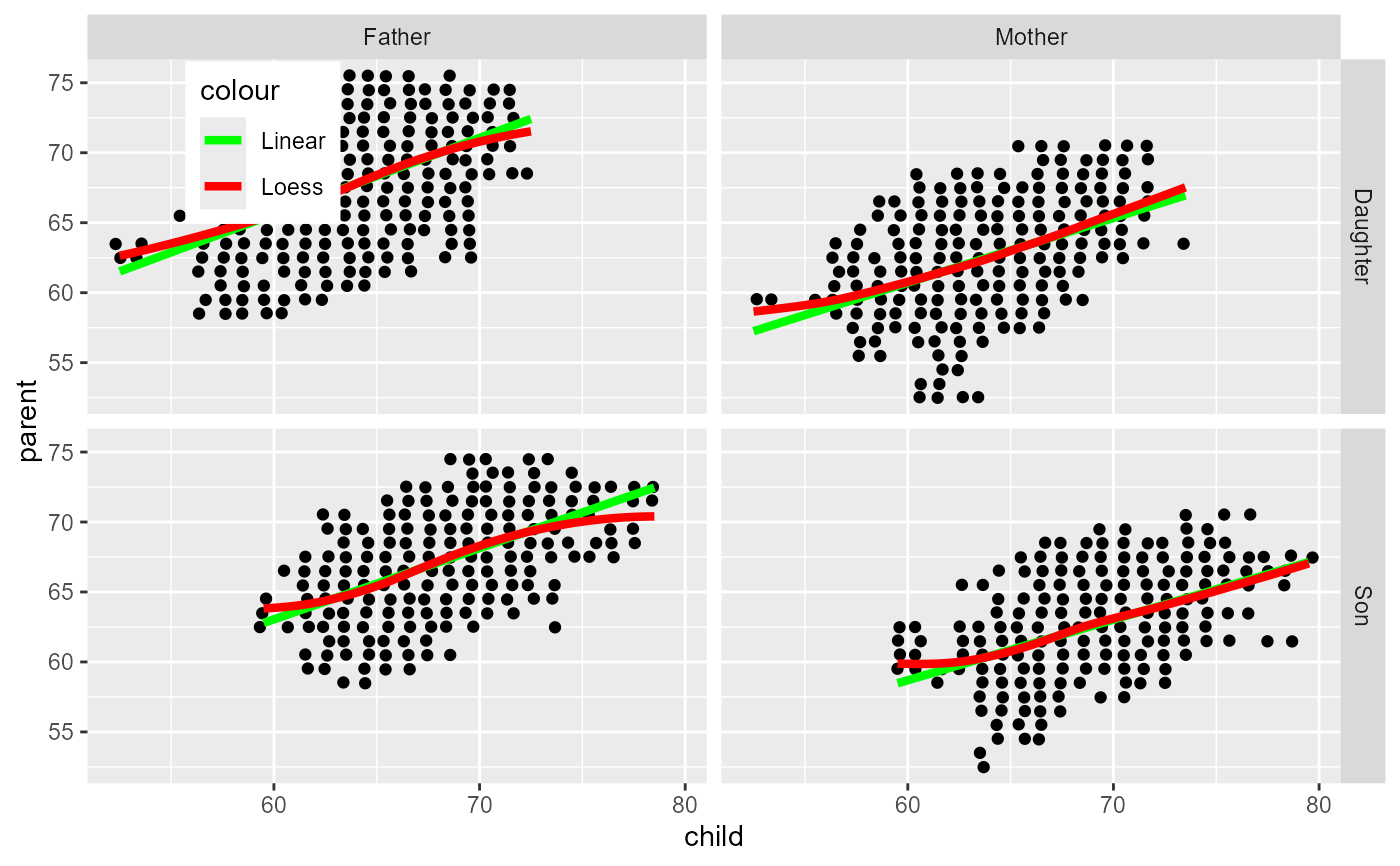
 # inverse regression, as in Wachmuth et al. (2003)
ggplot(PearsonLee, aes(x = child, y = parent, weight=frequency)) +
geom_point(size = 1.5, position = position_jitter(width = 0.2)) +
geom_smooth(method = lm, aes(weight = PearsonLee$frequency,
colour = 'Linear'), se = FALSE, size = 1.5) +
geom_smooth(aes(weight = PearsonLee$frequency,
colour = 'Loess'), se = FALSE, size = 1.5) +
facet_grid(chl ~ par) +
scale_colour_manual(breaks = c('Linear', 'Loess'),
values = c('green', 'red')) +
theme(legend.position = c(0.14, 0.885),
legend.background = element_rect(fill = 'white'))
#> Warning: Use of `PearsonLee$frequency` is discouraged.
#> ℹ Use `frequency` instead.
#> Warning: Use of `PearsonLee$frequency` is discouraged.
#> ℹ Use `frequency` instead.
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
# inverse regression, as in Wachmuth et al. (2003)
ggplot(PearsonLee, aes(x = child, y = parent, weight=frequency)) +
geom_point(size = 1.5, position = position_jitter(width = 0.2)) +
geom_smooth(method = lm, aes(weight = PearsonLee$frequency,
colour = 'Linear'), se = FALSE, size = 1.5) +
geom_smooth(aes(weight = PearsonLee$frequency,
colour = 'Loess'), se = FALSE, size = 1.5) +
facet_grid(chl ~ par) +
scale_colour_manual(breaks = c('Linear', 'Loess'),
values = c('green', 'red')) +
theme(legend.position = c(0.14, 0.885),
legend.background = element_rect(fill = 'white'))
#> Warning: Use of `PearsonLee$frequency` is discouraged.
#> ℹ Use `frequency` instead.
#> Warning: Use of `PearsonLee$frequency` is discouraged.
#> ℹ Use `frequency` instead.
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'