Student's (1906) Yeast Cell Counts

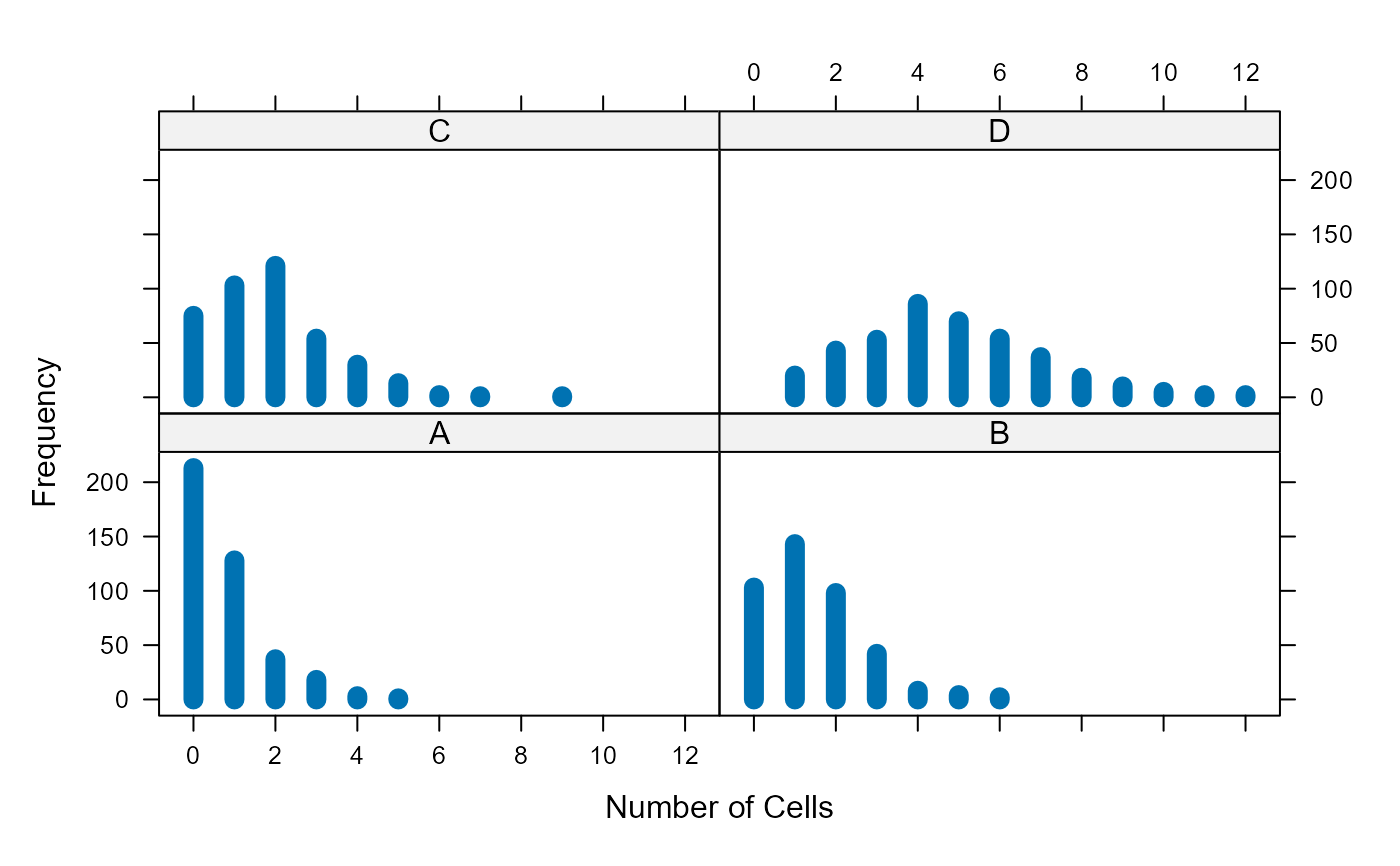
Counts of the number of yeast cells were made each of 400 regions in a 20 x 20 grid on a microscope slide, comprising a 1 sq. mm. area. This experiment was repeated four times, giving samples A, B, C and D.

Student (1906) used these data to investigate the errors in random sampling. He says "there are two sources of error: (a) the drop taken may not be representative of the bulk of the liquid; (b) the distribution of the cells over the area which is examined is never exactly uniform, so that there is an 'error of random sampling.'"

The data in the paper are provided in the form of discrete frequency distributions for the four samples. Each shows the frequency distribution squares containing a count of 0, 1, 2, ... yeast cells. These are combined here in Yeast. In addition, he gives a table (Table I) showing the actual number of yeast cells counted in the 20 x 20 grid for sample D, given here as YeastD.mat.

Format

Yeast: A frequency data frame with 36 observations on the following 3 variables, giving the frequencies of

sample

Sample identifier, a factor with levels A B C D

count

The number of yeast cells counted in a square

freq

The number of squares with the given count

YeastD.mat: A 20 x 20 matrix containing the count of yeast cells in each square for sample D.

Source

D. J. Hand, F. Daly, D. Lunn, K. McConway and E. Ostrowski (1994). A Handbook of Small Data Sets. London: Chapman & Hall. The data were originally found at: https://www2.stat.duke.edu/courses/Spring98/sta113/Data/Hand/yeast.dat

Details

Student considers the distribution of a total of \(Nm\) particles distributed over \(N\) unit areas with an average of \(m\) particles per unit area. With uniform mixing, for a given particle, the probability of it falling on any one area is \(p = 1/N\), and not falling on that area is \(q = 1 - 1/N\). He derives the probability distribution of 0, 1, 2, 3, ... particles on a single unit area from the binomial expansion of \((p + q)^{mN}\).

References

"Student" (1906) On the error of counting with a haemocytometer. Biometrika, 5, 351-360. https://jhanley.biostat.mcgill.ca/bios601/Intensity-Rate/Student_counting.pdf

See the example by John Russell for the 30DayChartChallenge

Examples

data(Yeast)

require(lattice)
# basic bar charts 
# TODO: frequencies should start at 0, not 1.
barchart(count~freq|sample, data=Yeast, ylab="Number of Cells", xlab="Frequency")

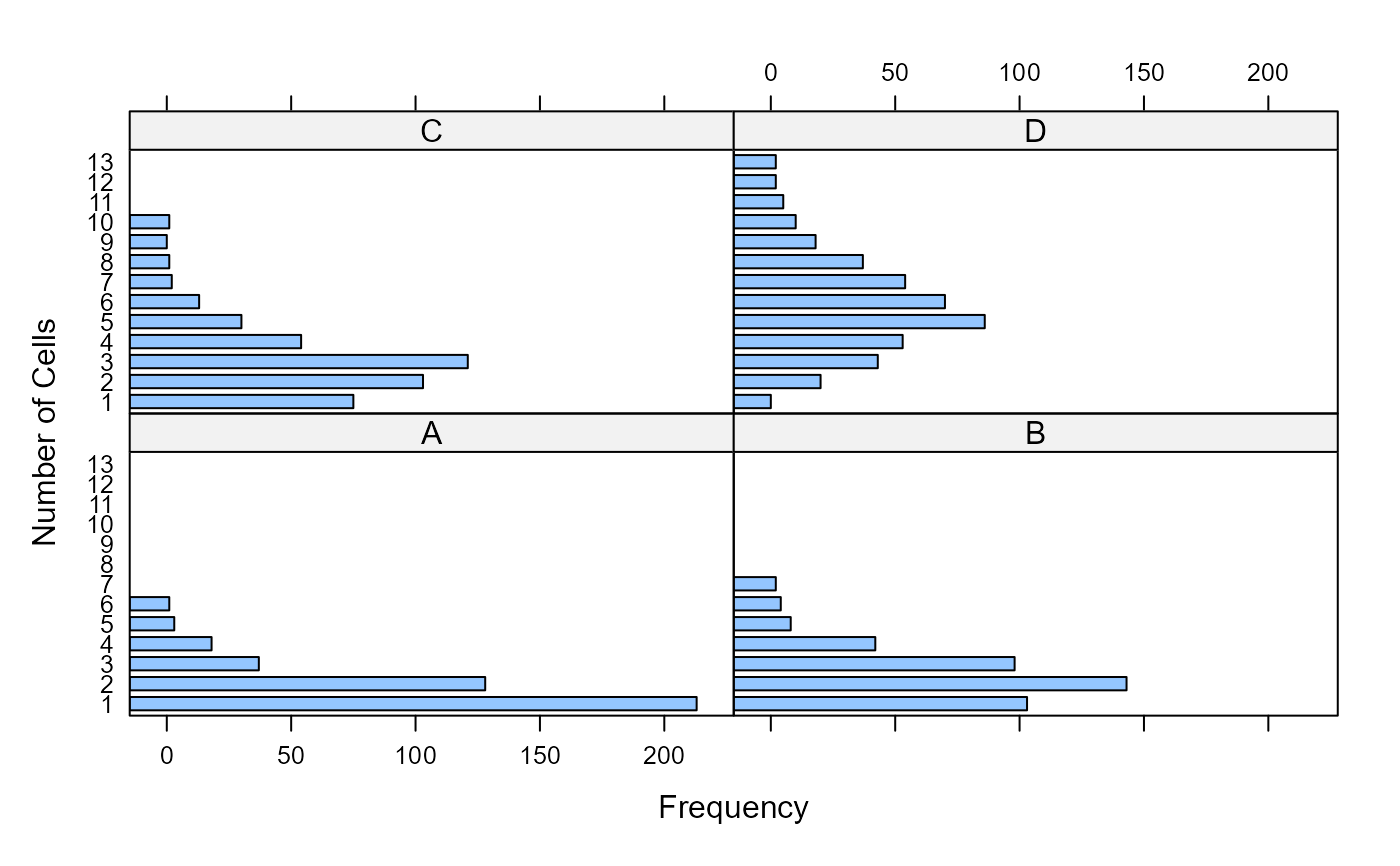barchart(freq~count|sample, data=Yeast, xlab="Number of Cells", ylab="Frequency",
  horizontal=FALSE, origin=0)


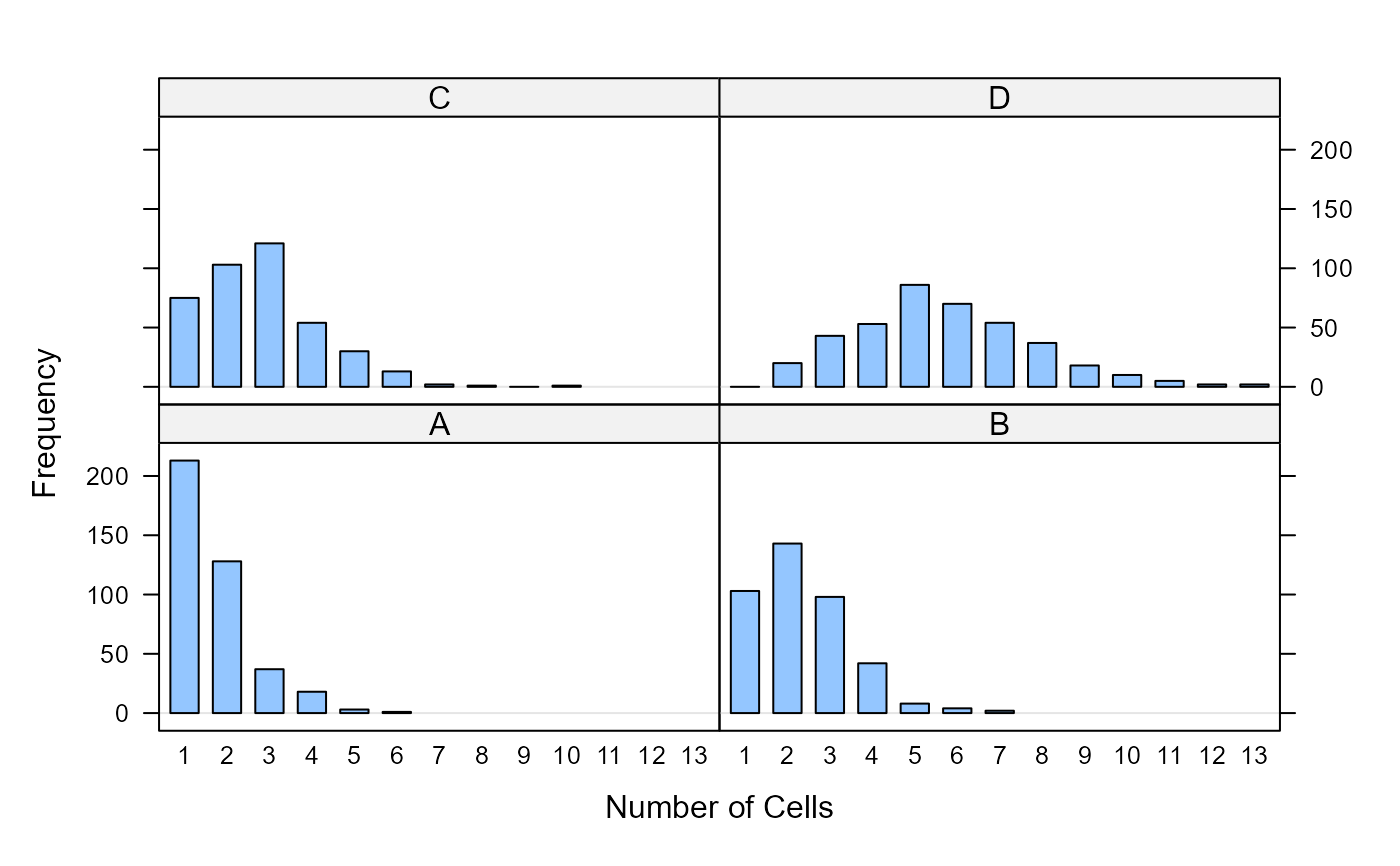# same, using xyplot
xyplot(freq~count|sample, data=Yeast, xlab="Number of Cells", ylab="Frequency",
  horizontal=FALSE, origin=0, type="h", lwd=10)