Canonical Correlation Plots

This function produces plots to help visualize X, Y data in canonical space.

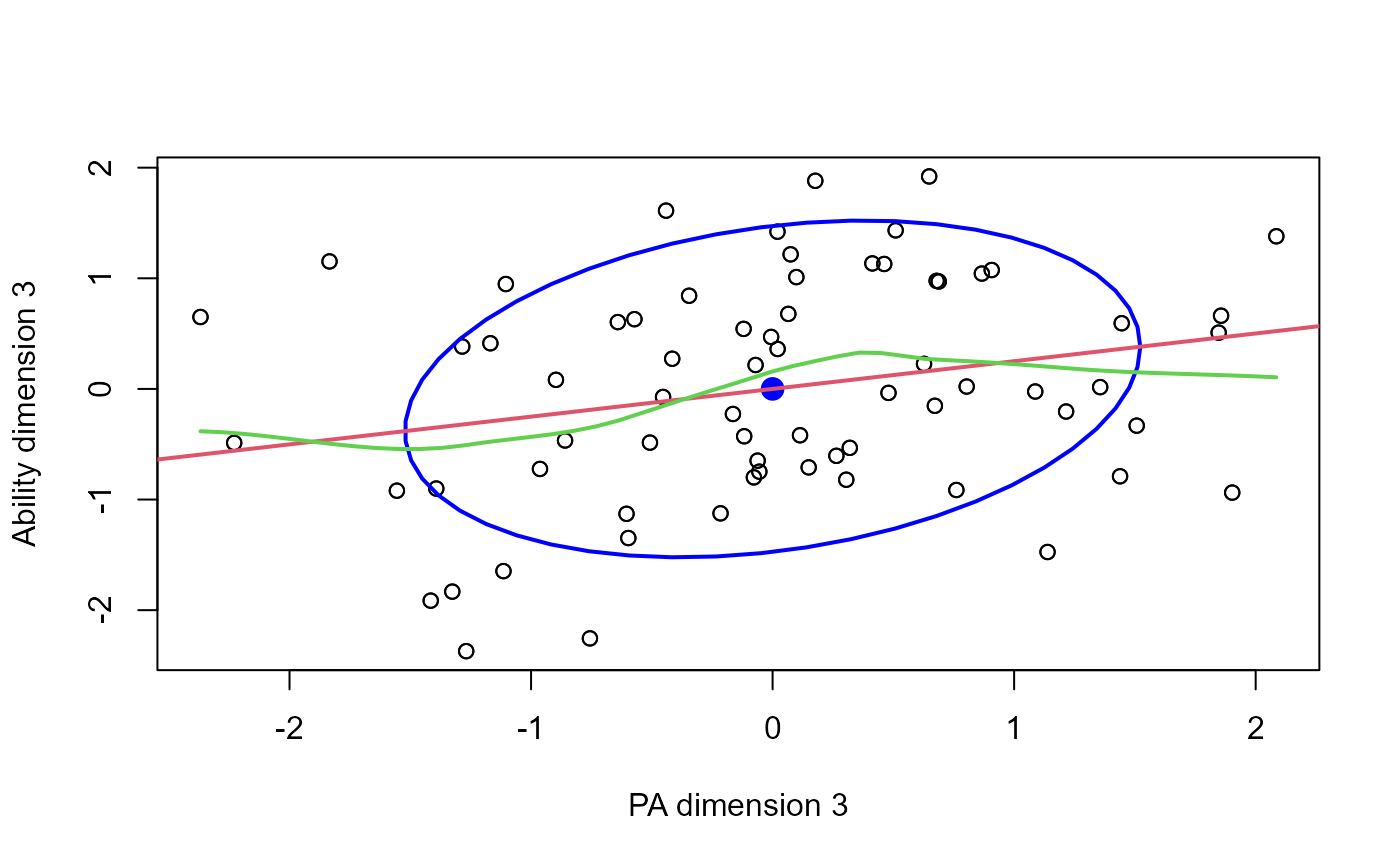
The present implementation plots the canonical scores for the Y variables against those for the X variables on given dimensions. We treat this as a view of the data in canonical space, and so offer additional annotations to a standard scatterplot.

Canonical correlation analysis assumes that the all correlations between the X and Y variables can be expressed in terms of correlations the canonical variate pairs, (Xcan1, Ycan1), (Xcan2, Ycan2), ..., and that the relations between these pairs are indeed linear.

Data ellipses, and smoothed (loess) curves, together with the linear regression line for each canonical dimension help to assess whether there are peculiarities in the data that might threaten the validity of CCA. Point identification methods can be useful to determine influential cases.

Usage

# S3 method for cancor
plot(
  x,
  which = 1,
  xlim,
  ylim,
  xlab,
  ylab,
  points = TRUE,
  add = FALSE,
  col = palette()[1],
  ellipse = TRUE,
  ellipse.args = list(),
  smooth = FALSE,
  smoother.args = list(),
  col.smooth = palette()[3],
  abline = TRUE,
  col.lines = palette()[2],
  lwd = 2,
  labels = rownames(xy),
  id.method = "mahal",
  id.n = 0,
  id.cex = 1,
  id.col = palette()[1],
  ...
)

Arguments

x: A "cancor" object
which: Which dimension to plot? An integer in 1:x$ndim.
xlim, ylim: Limits for x and y axes
xlab, ylab: Labels for x and y axes. If not specified, these are constructed from the set.names component of x.
points: logical. Display the points?
add: logical. Add to an existing plot?
col: Color for points.
ellipse: logical. Draw a data ellipse for the canonical scores?
ellipse.args: A list of arguments passed to dataEllipse. Internally, the function sets the default value for levels to 0.68.
smooth: logical. Draw a (loess) smoothed curve?
smoother.args: Arguments passed to loessLine, which should be consulted for details and defaults.
col.smooth: Color for the smoothed curve.
abline: logical. Draw the linear regression line for Ycan[,which] on Xcan[,which]?
col.lines: Color for the linear regression line
lwd: Line widths
labels: Point labels for point identification via the id.method argument.
id.method: Method used to identify individual points. See showLabels for details. The default, id.method = "mahal" identifies the id.n points furthest from the centroid.
id.n: Number of points to identify
id.cex, id.col: Character size and color for labeled points
...: Other arguments passed down to plot(...) and points(...)

Value

None. Used for its side effect of producing a plot.

the value returned

References

Mardia, K. V., Kent, J. T. and Bibby, J. M. (1979). Multivariate Analysis. London: Academic Press.

Author

Michael Friendly

Examples


data(Rohwer, package="heplots")
X <- as.matrix(Rohwer[,6:10])  # the PA tests
Y <- as.matrix(Rohwer[,3:5])   # the aptitude/ability variables

cc <- cancor(X, Y, set.names=c("PA", "Ability"))

plot(cc)

# exercise some options
plot(cc, which=1,
     smooth=TRUE, 
     pch = 16,
     id.n=3, ellipse.args=list(fill=TRUE, fill.alpha = 0.2))

plot(cc, which=2, smooth=TRUE)

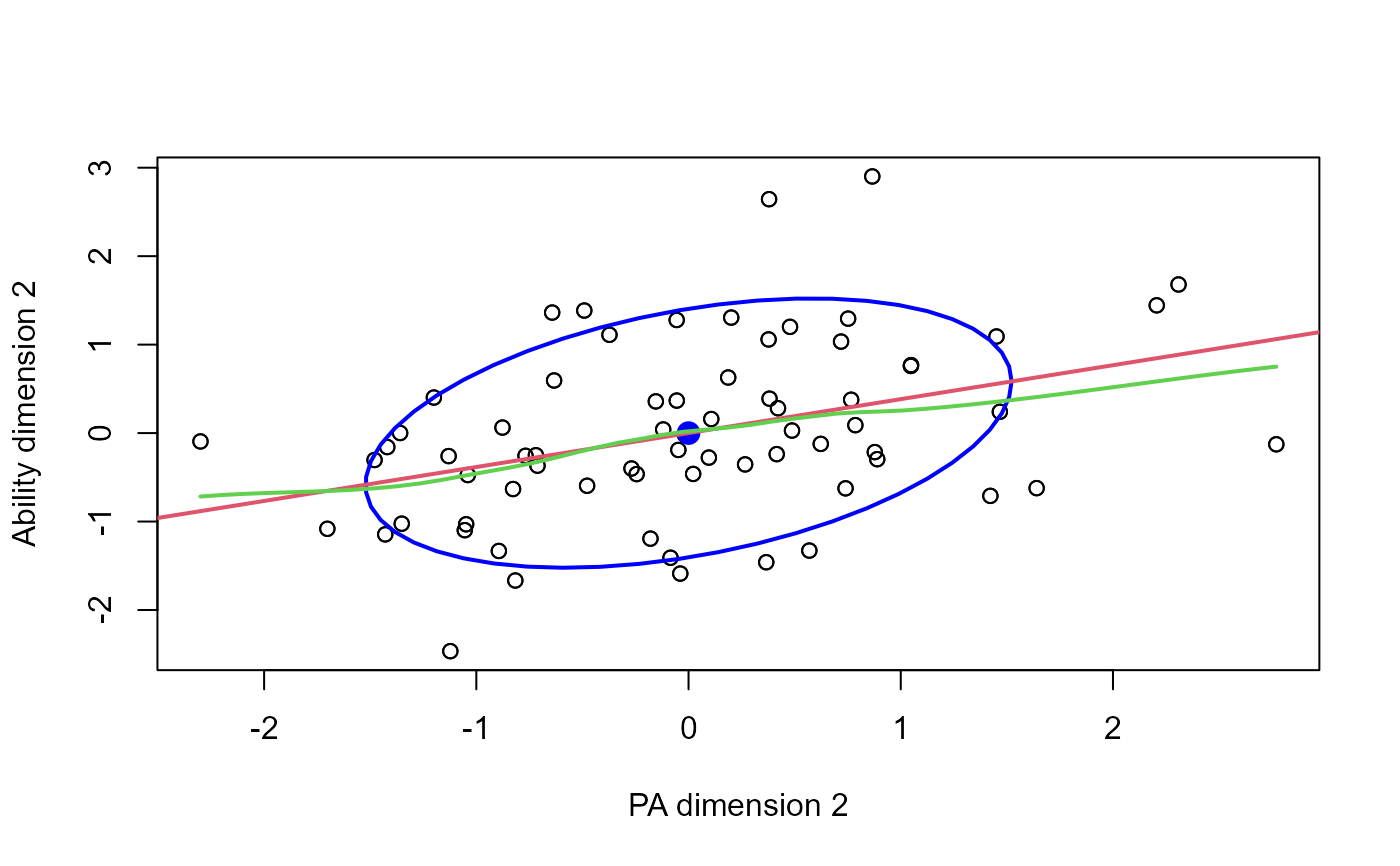plot(cc, which=3, smooth=TRUE)



# plot vectors showing structure correlations of Xcan and Ycan with their own variables
plot(cc)
struc <- cc$structure
Xstruc <- struc$X.xscores[,1]
Ystruc <- struc$Y.yscores[,1]
scale <- 2

# place vectors in the margins of the plot
usr <- matrix(par("usr"), nrow=2, dimnames=list(c("min", "max"), c("x", "y")))
ypos <- usr[2,2] - (1:5)/10 
arrows(0, ypos, scale*Xstruc, ypos, angle=10, len=0.1, col="blue")
text(scale*Xstruc, ypos, names(Xstruc), pos=2, col="blue")

xpos <- usr[2,1] - ( 1 + 1:3)/10
arrows(xpos, 0, xpos, scale*Ystruc, angle=10, len=0.1, col="darkgreen")
text(xpos, scale*Ystruc, names(Ystruc), pos=1, col="darkgreen")