Box's M-test for Homogeneity of Covariance Matrices

boxM() performs the Box's (1949) M-test for homogeneity of covariance matrices obtained from multivariate normal data according to one or more classification factors. The test compares the product of the log determinants of the separate covariance matrices to the log determinant of the pooled covariance matrix, analogous to a likelihood ratio test. The test statistic uses a chi-square approximation.

Usage

boxM(Y, ...)

# S3 method for class 'formula'
boxM(Y, data, ...)

# S3 method for class 'lm'
boxM(Y, ...)

# Default S3 method
boxM(Y, group, ...)

# S3 method for class 'boxM'
print(x, ...)

# S3 method for class 'boxM'
summary(
  object,
  digits = getOption("digits") - 2,
  cov = FALSE,
  quiet = FALSE,
  ...
)

Arguments

Y: The response variable matrix for the default method, or a "mlm" or "formula" object for a multivariate linear model. If Y is a linear-model object or a formula, the variables on the right-hand-side of the model must all be factors and must be completely crossed, e.g., A:B
...: Other arguments passed down
data: A data frame containing the variables in the model. Used only for the formula method.
group: A vector specifying the groups. Used only for the default method.
x: a class "boxM" object, for the print() method
object: A "boxM" object, result of a call to boxM
digits: Number of digits in printed output
cov: Logical; if TRUE, the covariance matrices for each group and the pooled covariance matrix are printed
quiet: Logical; if TRUE, suppress printed output

Value

A list with class c("boxM", "htest") containing the following components:

statistic: the chi-square (approximate) statistic for Box's M test, where large values imply the covariance matrices differ.
parameter: the degrees of freedom for the test statistic.
p.value: the p-value of the test
ngroups: the number of levels of the group variable
cov: a list of the group covariance matrices, of length ngroups
pooled: the pooled covariance matrix
means: a matrix whose ngroups+1 rows are the means of the variables, followed by those for pooled data.
logDet: a vector of length ngroups+1 containing the natural logarithm of each matrix in cov, followed by that for the pooled covariance matrix
df: a vector of the degrees of freedom for all groups, followed by that for the pooled covariance matrix
data.name: a character string giving the names of the data, as extracted from the call
method: the character string "Box's M-test for Homogeneity of Covariance Matrices"

Details

As an object of class "boxM", a few methods are available: print.boxM(), summary.boxM() and plot.boxM().

There is no general provision as yet for handling missing data. Missing data are simply removed, with a warning.

As well, the computation assumes that the covariance matrix for each group is non-singular, so that \(\log det(S_i)\) can be calculated for each group. At the minimum, this requires that \(n > p\) for each group.

Box's M test for a multivariate linear model highly sensitive to departures from multivariate normality, just as the analogous univariate test. It is also affected adversely by unbalanced designs. Some people recommend to ignore the result unless it is very highly significant, e.g., p < .0001 or worse.

In general, heterogeneity of covariance matrices can be more easily seen and understood by plotting the covariance ellipses using covEllipses.

The summary method prints a variety of additional statistics based on the eigenvalues of the covariance matrices. These are returned invisibly, as a list containing the following components:

logDet

the vector of log determinants

eigs

eigenvalues of the covariance matrices

eigstats

statistics computed on the eigenvalues for each covariance matrix:

product: the product of eigenvalues, \(\prod{\lambda_i}\)
sum: the sum of eigenvalues, \(\sum{\lambda_i}\)
precision: the average precision of eigenvalues, \(1/\sum(1/\lambda_i)\)
max: the maximum eigenvalue, \(\lambda_1\)

References

Box, G. E. P. (1949). A general distribution theory for a class of likelihood criteria. Biometrika, 36, 317-346.

Morrison, D.F. (1976) Multivariate Statistical Methods.

Author

The default method was taken from the biotools package, Anderson Rodrigo da Silva anderson.agro@hotmail.com

Generalized by Michael Friendly and John Fox

Examples


data(iris)

# default method, using `Y`, `group` 
res <- boxM(iris[, 1:4], iris[, "Species"])
res
#> 
#>  Box's M-test for Homogeneity of Covariance Matrices 
#> 
#> data:  iris[, 1:4] by iris[, "Species"] 
#> Chi-Sq (approx.) = 140.943, df = 20, p-value = < 2.2e-16
#> 

# summary method gives details
summary(res)
#> 
#>  Box's M-test for Homogeneity of Covariance Matrices 
#> 
#> data:  iris[, 1:4] by iris[, "Species"] 
#> 
#> Chi-Sq (approx.) =  140.943 
#> df:	 20 
#> p-value: <2e-16 
#> 
#> log of Covariance determinants:
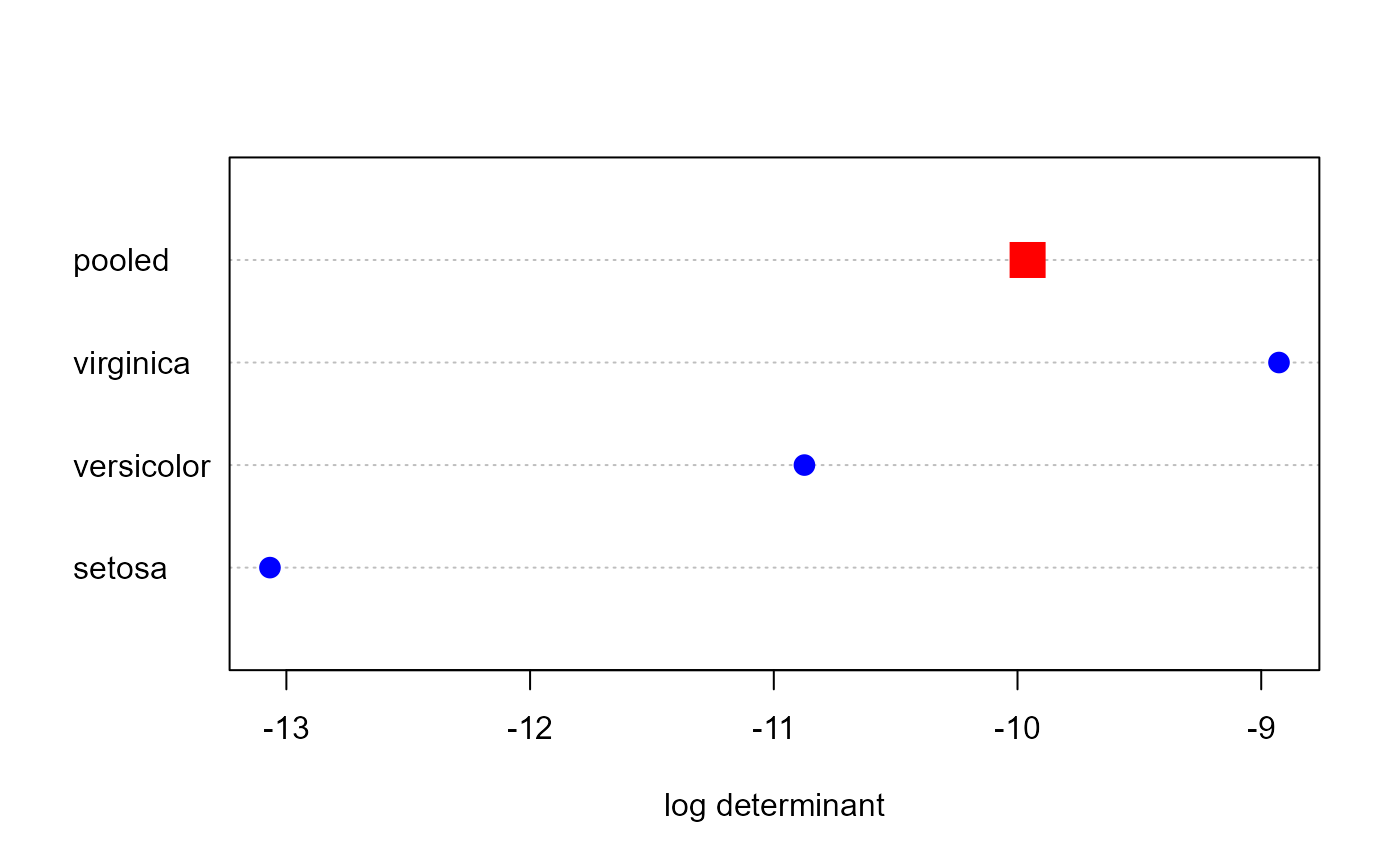
#>     setosa versicolor  virginica     pooled 
#>   -13.0674   -10.8743    -8.9271    -9.9585 
#> 
#> Eigenvalues:
#>      setosa versicolor virginica   pooled
#> 1 0.2364557  0.4878739  0.695255 0.443566
#> 2 0.0369187  0.0723841  0.106551 0.086183
#> 3 0.0267964  0.0547761  0.052295 0.055352
#> 4 0.0090333  0.0097904  0.034266 0.022364
#> 
#> Statistics based on eigenvalues:
#>               setosa versicolor  virginica     pooled
#> product   2.1131e-06 1.8938e-05 0.00013275 4.7322e-05
#> sum       3.0920e-01 6.2482e-01 0.88836735 6.0747e-01
#> precision 5.5761e-03 7.3388e-03 0.01691212 1.3048e-02
#> max       2.3646e-01 4.8787e-01 0.69525484 4.4357e-01

# visualize (this is what is done in the plot method)
dets <- res$logDet
ng <- length(res$logDet)-1
dotchart(dets, xlab = "log determinant")
points(dets , 1:4, cex=c(rep(1.5, ng), 2.5), pch=c(rep(16, ng), 15),
       col= c(rep("blue", ng), "red"))


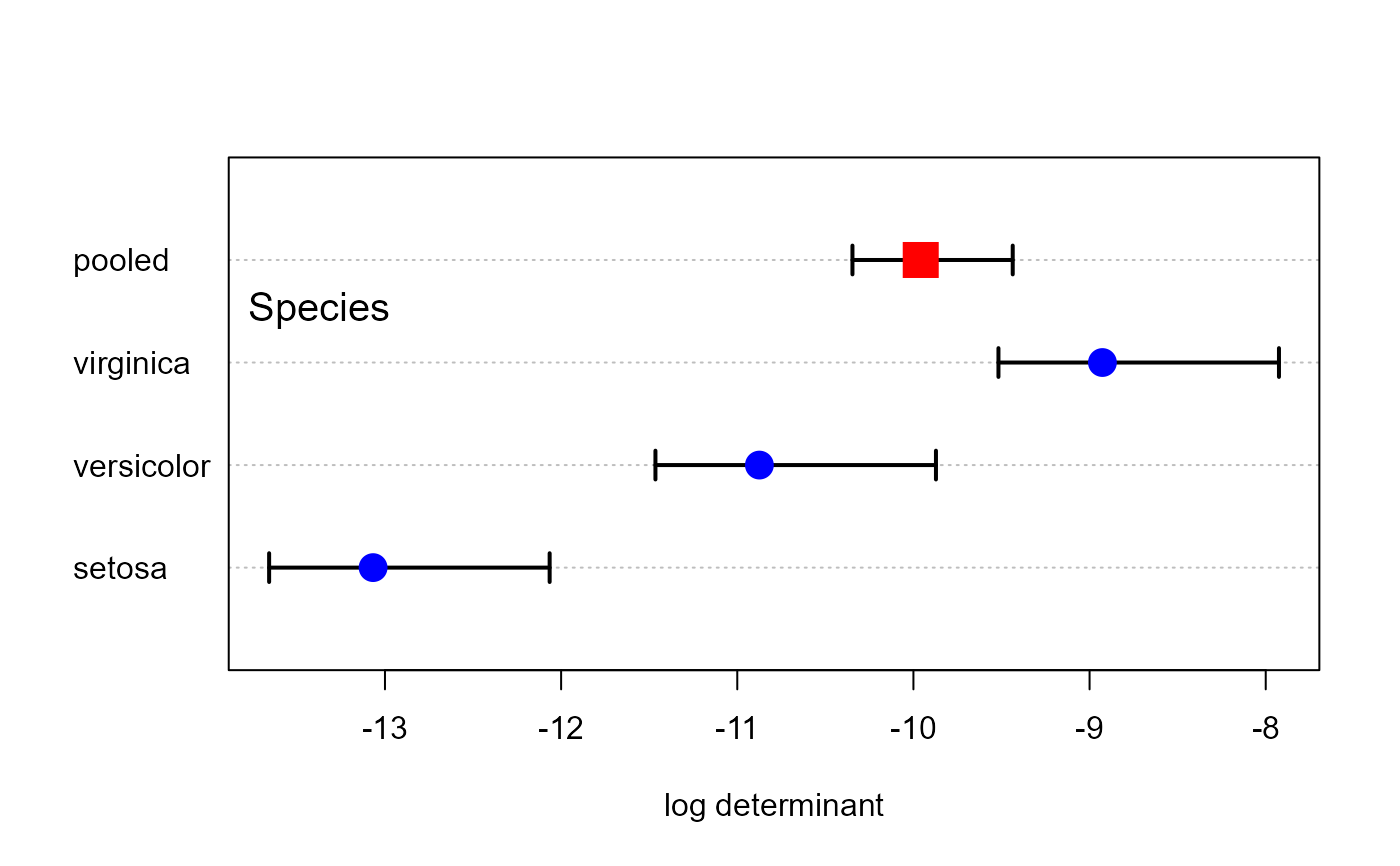
# plot method gives confidence intervals for logDet
plot(res, gplabel="Species")


# formula method
boxM( cbind(Sepal.Length, Sepal.Width, Petal.Length, Petal.Width) ~ Species,
      data=iris)
#> 
#>  Box's M-test for Homogeneity of Covariance Matrices 
#> 
#> data:  iris 
#> Chi-Sq (approx.) = 140.943, df = 20, p-value = < 2.2e-16
#> 

### Skulls data
data(Skulls)

# lm method
skulls.mod <- lm(cbind(mb, bh, bl, nh) ~ epoch, data=Skulls)
skulls.boxM <- boxM(skulls.mod) |>
  print()
#> 
#>  Box's M-test for Homogeneity of Covariance Matrices 
#> 
#> data:  Y by group 
#> Chi-Sq (approx.) = 45.6672, df = 40, p-value = 0.2483
#> 
summary(skulls.boxM)
#> 
#>  Box's M-test for Homogeneity of Covariance Matrices 
#> 
#> data:  Y by group 
#> 
#> Chi-Sq (approx.) =  45.66723 
#> df:	 40 
#> p-value: 0.25 
#> 
#> log of Covariance determinants:
#> c1850BC  c200BC c3300BC c4000BC  cAD150  pooled 
#>  11.222  10.469  11.032  11.477  12.153  11.605 
#> 
#> Eigenvalues:
#>   c1850BC  c200BC c3300BC c4000BC cAD150 pooled
#> 1  26.931 35.9064 28.3992 34.8234 37.332 29.462
#> 2  19.075 16.9560 22.0306 30.3339 28.600 21.441
#> 3  13.207 13.6751 15.5959 18.4358 14.800 18.779
#> 4  11.014  4.2292  6.3364  4.9517 12.003  9.246
#> 
#> Statistics based on eigenvalues:
#>              c1850BC     c200BC    c3300BC    c4000BC     cAD150     pooled
#> product   74729.0725 35211.6576 61827.9462 96431.2960 189666.582 1.0968e+05
#> sum          70.2276    70.7667    72.3621    88.5448     92.734 7.8927e+01
#> precision     3.9053     2.5227     3.3053     3.1459      4.703 4.1324e+00
#> max          26.9311    35.9064    28.3992    34.8234     37.332 2.9462e+01