Growth of Apple Trees from Different Root Stocks

In a classic experiment carried out from 1918 to 1934, growth of apple trees of six different rootstocks were compared on four measures of size. How do the measures of size vary with the type of rootstock?

Format

A data frame with 48 observations on the following 5 variables.

rootstock

a factor with levels 1 2 3 4 5 6

girth4

a numeric vector: trunk girth at 4 years (mm x 100)

ext4

a numeric vector: extension growth at 4 years (m)

girth15

a numeric vector: trunk girth at 15 years (mm x 100)

weight15

a numeric vector: weight of tree above ground at 15 years (lb x 1000)

Source

Andrews, D. and Herzberg, A. (1985). Data: A Collection of Problems from Many Fields for the Student and Research Worker Springer-Verlag, pp. 357–360.

Details

This is a balanced, one-way MANOVA design, with n=8 trees for each rootstock.

References

Rencher, A. C. (1995). Methods of Multivariate Analysis. New York: Wiley, Table 6.2

Examples

library(car)
data(RootStock)
str(RootStock)
#> 'data.frame':	48 obs. of  5 variables:
#>  $ rootstock: Factor w/ 6 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 2 2 ...
#>  $ girth4   : num  1.11 1.19 1.09 1.25 1.11 1.08 1.11 1.16 1.05 1.17 ...
#>  $ ext4     : num  2.57 2.93 2.87 3.84 3.03 ...
#>  $ girth15  : num  3.58 3.75 3.93 3.94 3.6 3.51 3.98 3.62 4.09 4.06 ...
#>  $ weight15 : num  0.76 0.821 0.928 1.009 0.766 ...

root.mod <- lm(cbind(girth4, ext4, girth15, weight15) ~ rootstock, data=RootStock)
car::Anova(root.mod)
#> 
#> Type II MANOVA Tests: Pillai test statistic
#>           Df test stat approx F num Df den Df    Pr(>F)    
#> rootstock  5    1.3055   4.0697     20    168 1.983e-07 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

pairs(root.mod)


# test two orthogonal contrasts among the rootstocks
hyp <- matrix(c(2,-1,-1,-1,-1,2,  
                1, 0,0,0,0,-1), 2, 6, byrow=TRUE)
car::linearHypothesis(root.mod, hyp)
#> 
#> Sum of squares and products for the hypothesis:
#>            girth4      ext4   girth15 weight15
#> girth4   2.684223  7.573365  7.792122 1.617892
#> ext4     7.573365 22.489458 23.293194 5.760003
#> girth15  7.792122 23.293194 24.145778 6.090615
#> weight15 1.617892  5.760003  6.090615 2.248755
#> 
#> Sum of squares and products for error:
#>             girth4      ext4   girth15 weight15
#> girth4   0.3199875  1.696564 0.5540875 0.217140
#> ext4     1.6965637 12.142790 4.3636125 2.110214
#> girth15  0.5540875  4.363612 4.2908125 2.481656
#> weight15 0.2171400  2.110214 2.4816562 1.722525
#> 
#> Multivariate Tests: 
#>                  Df test stat  approx F num Df den Df     Pr(>F)    
#> Pillai            2  1.426293  24.86102      8     80 < 2.22e-16 ***
#> Wilks             2  0.020401  58.51245      8     78 < 2.22e-16 ***
#> Hotelling-Lawley  2 26.121884 124.07895      8     76 < 2.22e-16 ***
#> Roy               2 25.254884 252.54884      4     40 < 2.22e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
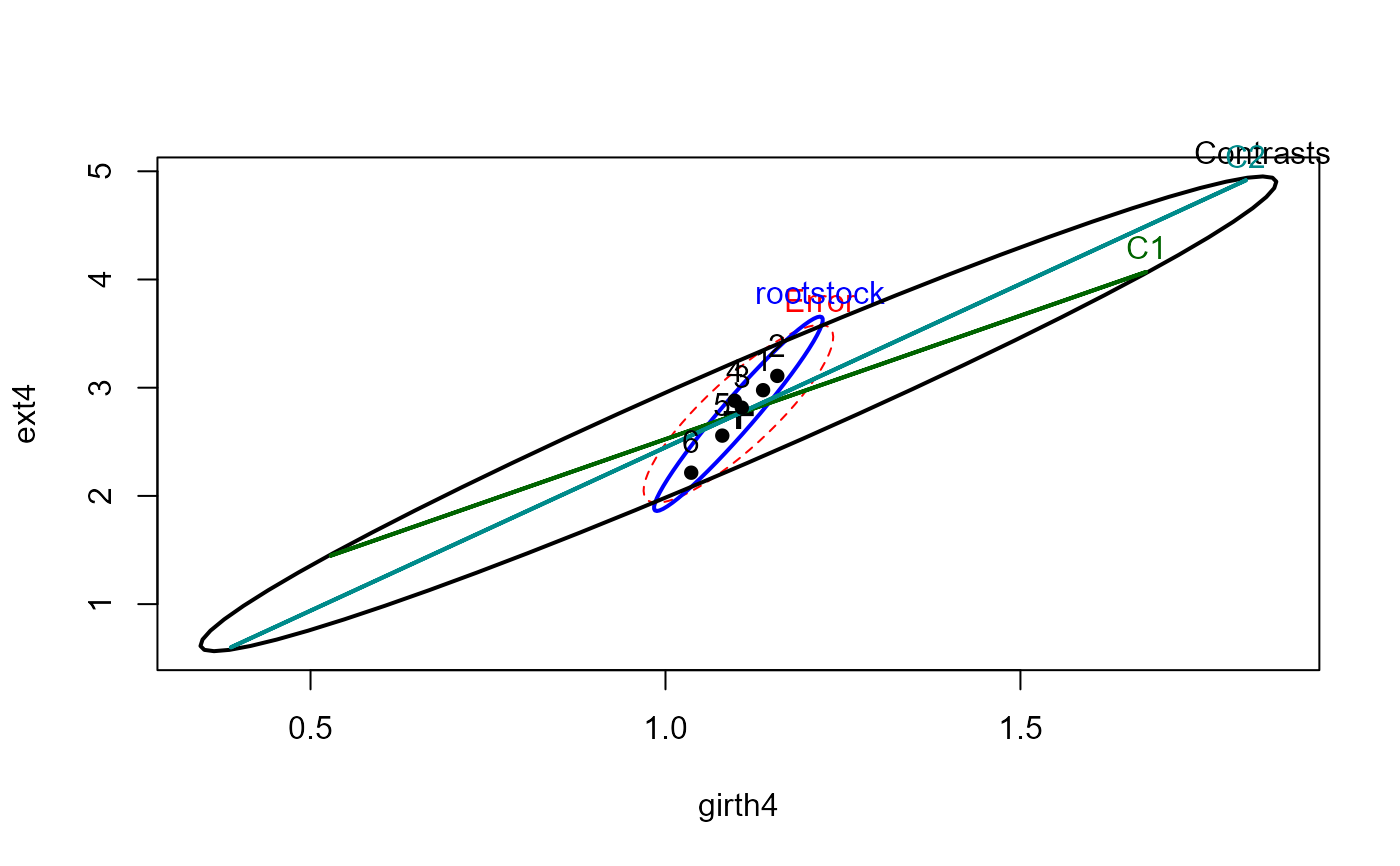
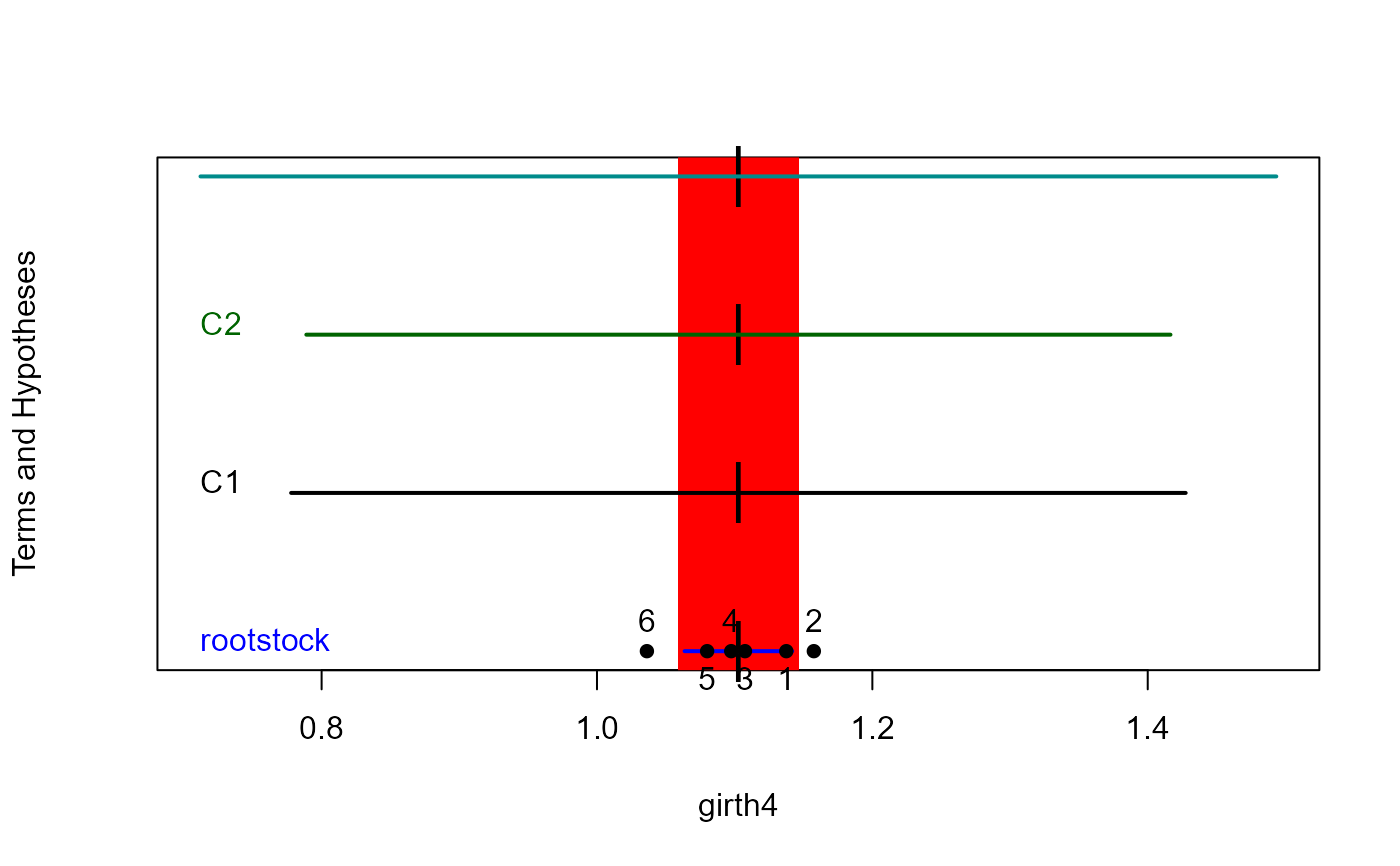
heplot(root.mod, hypotheses=list(Contrasts=hyp, C1=hyp[1,], C2=hyp[2,]))


heplot1d(root.mod, hypotheses=list(Contrasts=hyp, C1=hyp[1,], C2=hyp[2,]))