Skip to contents

Gaussian Elimination

Source: R/gaussian-elimination.R
gaussianElimination.Rd

gaussianElimination demonstrates the algorithm of row reduction used for solving systems of linear equations of the form \(A x = B\). Optional arguments verbose and fractions may be used to see how the algorithm works.

Usage

gaussianElimination(
  A,
  B,
  tol = sqrt(.Machine$double.eps),
  verbose = FALSE,
  latex = FALSE,
  fractions = FALSE
)

# S3 method for class 'enhancedMatrix'
print(x, ...)

Arguments

A

coefficient matrix

B

right-hand side vector or matrix. If B is a matrix, the result gives solutions for each column as the right-hand side of the equations with coefficients in A.

tol

tolerance for checking for 0 pivot

verbose

logical; if TRUE, print intermediate steps

latex

logical; if TRUE, and verbose is TRUE, print intermediate steps using LaTeX equation outputs rather than R output

fractions

logical; if TRUE, try to express non-integers as rational numbers, using the fractions function; if you require greater accuracy, you can set the cycles (default 10) and/or max.denominator (default 2000) arguments to fractions as a global option, e.g., options(fractions=list(cycles=100, max.denominator=10^4)).

x

matrix to print

...

arguments to pass down

Value

If B is absent, returns the reduced row-echelon form of A. If B is present, returns the reduced row-echelon form of A, with the same operations applied to B.

Author

John Fox

Examples

  A <- matrix(c(2, 1, -1,
               -3, -1, 2,
               -2,  1, 2), 3, 3, byrow=TRUE)
  b <- c(8, -11, -3)
  gaussianElimination(A, b)
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    0    0    2
#> [2,]    0    1    0    3
#> [3,]    0    0    1   -1
  gaussianElimination(A, b, verbose=TRUE, fractions=TRUE)
#> 
#> Initial matrix:
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]   2    1   -1    8 
#> [2,]  -3   -1    2  -11 
#> [3,]  -2    1    2   -3 
#> 
#> row: 1 
#> 
#>  exchange rows 1 and 2 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]  -3   -1    2  -11 
#> [2,]   2    1   -1    8 
#> [3,]  -2    1    2   -3 
#> 
#>  multiply row 1 by -1/3 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1  1/3 -2/3 11/3
#> [2,]    2    1   -1    8
#> [3,]   -2    1    2   -3
#> 
#>  multiply row 1 by 2 and subtract from row 2 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1  1/3 -2/3 11/3
#> [2,]    0  1/3  1/3  2/3
#> [3,]   -2    1    2   -3
#> 
#>  multiply row 1 by 2 and add to row 3 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1  1/3 -2/3 11/3
#> [2,]    0  1/3  1/3  2/3
#> [3,]    0  5/3  2/3 13/3
#> 
#> row: 2 
#> 
#>  exchange rows 2 and 3 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1  1/3 -2/3 11/3
#> [2,]    0  5/3  2/3 13/3
#> [3,]    0  1/3  1/3  2/3
#> 
#>  multiply row 2 by 3/5 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1  1/3 -2/3 11/3
#> [2,]    0    1  2/5 13/5
#> [3,]    0  1/3  1/3  2/3
#> 
#>  multiply row 2 by 1/3 and subtract from row 1 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    0 -4/5 14/5
#> [2,]    0    1  2/5 13/5
#> [3,]    0  1/3  1/3  2/3
#> 
#>  multiply row 2 by 1/3 and subtract from row 3 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    0 -4/5 14/5
#> [2,]    0    1  2/5 13/5
#> [3,]    0    0  1/5 -1/5
#> 
#> row: 3 
#> 
#>  multiply row 3 by 5 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    0 -4/5 14/5
#> [2,]    0    1  2/5 13/5
#> [3,]    0    0    1   -1
#> 
#>  multiply row 3 by 4/5 and add to row 1 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    0    0    2
#> [2,]    0    1  2/5 13/5
#> [3,]    0    0    1   -1
#> 
#>  multiply row 3 by 2/5 and subtract from row 2 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#>      [,1] [,2] [,3] [,4]
#> [1,]  1    0    0    2  
#> [2,]  0    1    0    3  
#> [3,]  0    0    1   -1  
  gaussianElimination(A, b, verbose=TRUE, fractions=TRUE, latex=TRUE)
#> 
#> Initial matrix:
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   2 & 1 & -1 & 8 \\ 
#>   -3 & -1 & 2 & -11 \\ 
#>   -2 & 1 & 2 & -3 \\ 
#>   \end{array} \right]
#> 
#> row: 1 
#> 
#>  exchange rows 1 and 2 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   -3 & -1 & 2 & -11 \\ 
#>   2 & 1 & -1 & 8 \\ 
#>   -2 & 1 & 2 & -3 \\ 
#>   \end{array} \right]
#> 
#>  multiply row 1 by -1/3 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 1/3 & -2/3 & 11/3 \\ 
#>   2 & 1 & -1 & 8 \\ 
#>   -2 & 1 & 2 & -3 \\ 
#>   \end{array} \right]
#> 
#>  multiply row 1 by 2 and subtract from row 2 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 1/3 & -2/3 & 11/3 \\ 
#>   0 & 1/3 & 1/3 & 2/3 \\ 
#>   -2 & 1 & 2 & -3 \\ 
#>   \end{array} \right]
#> 
#>  multiply row 1 by 2 and add to row 3 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 1/3 & -2/3 & 11/3 \\ 
#>   0 & 1/3 & 1/3 & 2/3 \\ 
#>   0 & 5/3 & 2/3 & 13/3 \\ 
#>   \end{array} \right]
#> 
#> row: 2 
#> 
#>  exchange rows 2 and 3 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 1/3 & -2/3 & 11/3 \\ 
#>   0 & 5/3 & 2/3 & 13/3 \\ 
#>   0 & 1/3 & 1/3 & 2/3 \\ 
#>   \end{array} \right]
#> 
#>  multiply row 2 by 3/5 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 1/3 & -2/3 & 11/3 \\ 
#>   0 & 1 & 2/5 & 13/5 \\ 
#>   0 & 1/3 & 1/3 & 2/3 \\ 
#>   \end{array} \right]
#> 
#>  multiply row 2 by 1/3 and subtract from row 1 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 0 & -4/5 & 14/5 \\ 
#>   0 & 1 & 2/5 & 13/5 \\ 
#>   0 & 1/3 & 1/3 & 2/3 \\ 
#>   \end{array} \right]
#> 
#>  multiply row 2 by 1/3 and subtract from row 3 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 0 & -4/5 & 14/5 \\ 
#>   0 & 1 & 2/5 & 13/5 \\ 
#>   0 & 0 & 1/5 & -1/5 \\ 
#>   \end{array} \right]
#> 
#> row: 3 
#> 
#>  multiply row 3 by 5 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 0 & -4/5 & 14/5 \\ 
#>   0 & 1 & 2/5 & 13/5 \\ 
#>   0 & 0 & 1 & -1 \\ 
#>   \end{array} \right]
#> 
#>  multiply row 3 by 4/5 and add to row 1 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 0 & 0 & 2 \\ 
#>   0 & 1 & 2/5 & 13/5 \\ 
#>   0 & 0 & 1 & -1 \\ 
#>   \end{array} \right]
#> 
#>  multiply row 3 by 2/5 and subtract from row 2 
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> Warning: Function is deprecated. See latexMatrix() and Eqn() for more recent approaches
#> \left[
#>  \begin{array}{llll}
#>   1 & 0 & 0 & 2 \\ 
#>   0 & 1 & 0 & 3 \\ 
#>   0 & 0 & 1 & -1 \\ 
#>   \end{array} \right]

  # determine whether matrix is solvable
  gaussianElimination(A, numeric(3))
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    0    0    0
#> [2,]    0    1    0    0
#> [3,]    0    0    1    0

  # find inverse matrix by elimination: A = I -> A^-1 A = A^-1 I -> I = A^-1
  gaussianElimination(A, diag(3))
#>      [,1] [,2] [,3] [,4] [,5] [,6]
#> [1,]    1    0    0    4    3   -1
#> [2,]    0    1    0   -2   -2    1
#> [3,]    0    0    1    5    4   -1
  inv(A)
#>      [,1] [,2] [,3]
#> [1,]    4    3   -1
#> [2,]   -2   -2    1
#> [3,]    5    4   -1

  # works for 1-row systems (issue # 30)
  A2 <- matrix(c(1, 1), nrow=1)
  b2 = 2
  gaussianElimination(A2, b2)
#>      [,1] [,2] [,3]
#> [1,]    1    1    2
  showEqn(A2, b2)
#> 1*x1 + 1*x2  =  2 
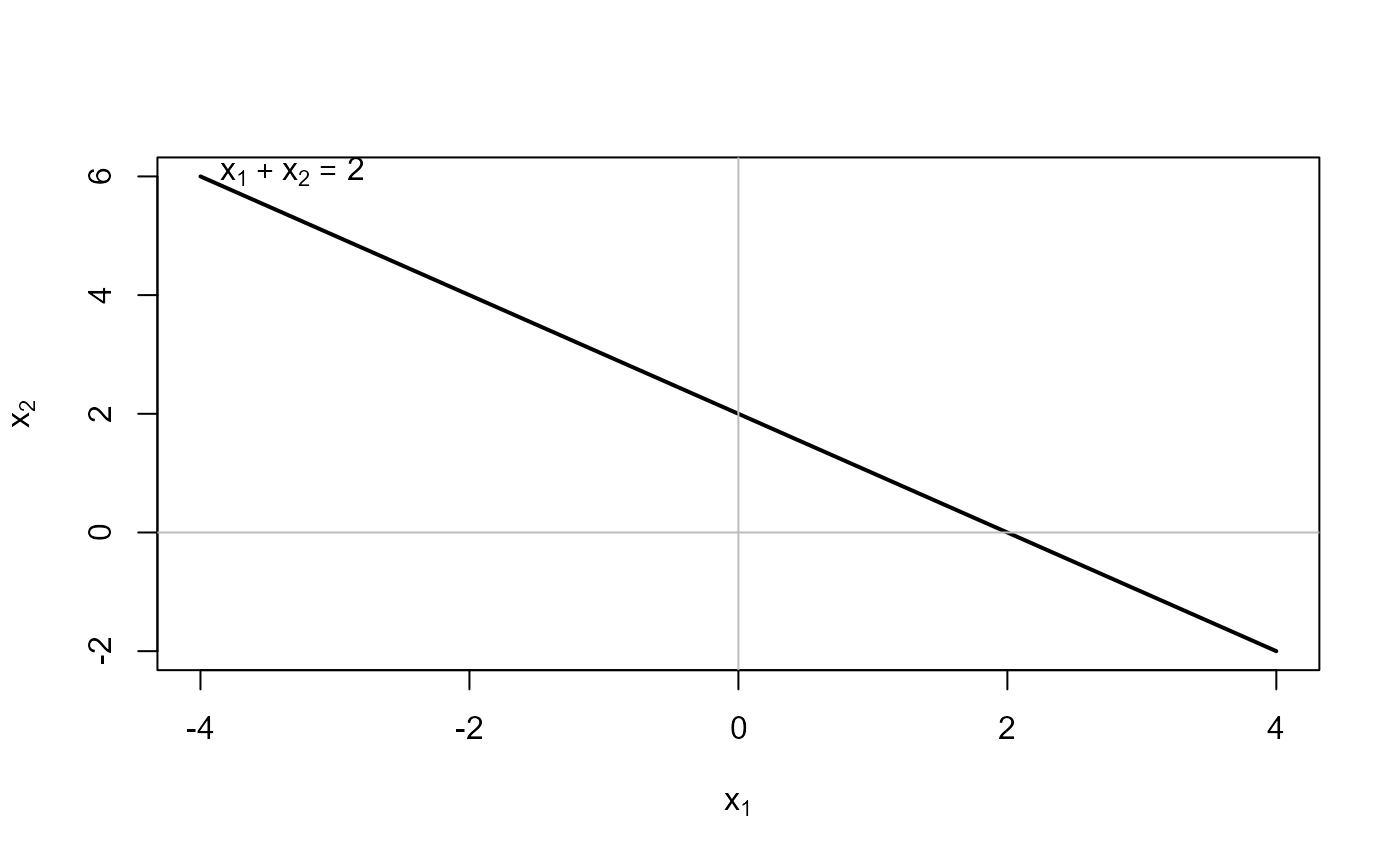
  # plotEqn works for this case
  plotEqn(A2, b2)
#> x[1] + x[2]  =  2