Plot Linear Equations

Shows what matrices \(A, b\) look like as the system of linear equations, \(A x = b\) with two unknowns, x1, x2, by plotting a line for each equation.

Usage

plotEqn(
  A,
  b,
  vars,
  xlim,
  ylim,
  col = 1:nrow(A),
  lwd = 2,
  lty = 1,
  axes = TRUE,
  labels = TRUE,
  solution = TRUE,
  ...
)

Arguments

A

either the matrix of coefficients of a system of linear equations, or the matrix cbind(A,b). The A matrix must have two columns.

b

if supplied, the vector of constants on the right hand side of the equations, of length matching the number of rows of A.

vars

a numeric or character vector of names of the variables. If supplied, the length must be equal to the number of unknowns in the equations, i.e., 2. The default is c(expression(x[1]), expression(x[2])).

xlim

horizontal axis limits for the first variable

ylim

vertical axis limits for the second variable; if missing, ylim is calculated from the range of the set of equations over the xlim.

col

scalar or vector of colors for the lines, recycled as necessary

lwd

scalar or vector of line widths for the lines, recycled as necessary

lty

scalar or vector of line types for the lines, recycled as necessary

axes

logical; draw horizontal and vertical axes through (0,0)?

labels

logical, or a vector of character labels for the equations; if TRUE, each equation is labeled using the character string resulting from showEqn, modified so that the xs are properly subscripted.

solution

logical; should the solution points for pairs of equations be marked?

...

Other arguments passed to plot

Value

nothing; used for the side effect of making a plot

References

Fox, J. and Friendly, M. (2016). "Visualizing Simultaneous Linear Equations, Geometric Vectors, and Least-Squares Regression with the matlib Package for R". useR Conference, Stanford, CA, June 27 - June 30, 2016.

See also

showEqn, vignette("linear-equations", package="matlib")

Author

Michael Friendly

Examples

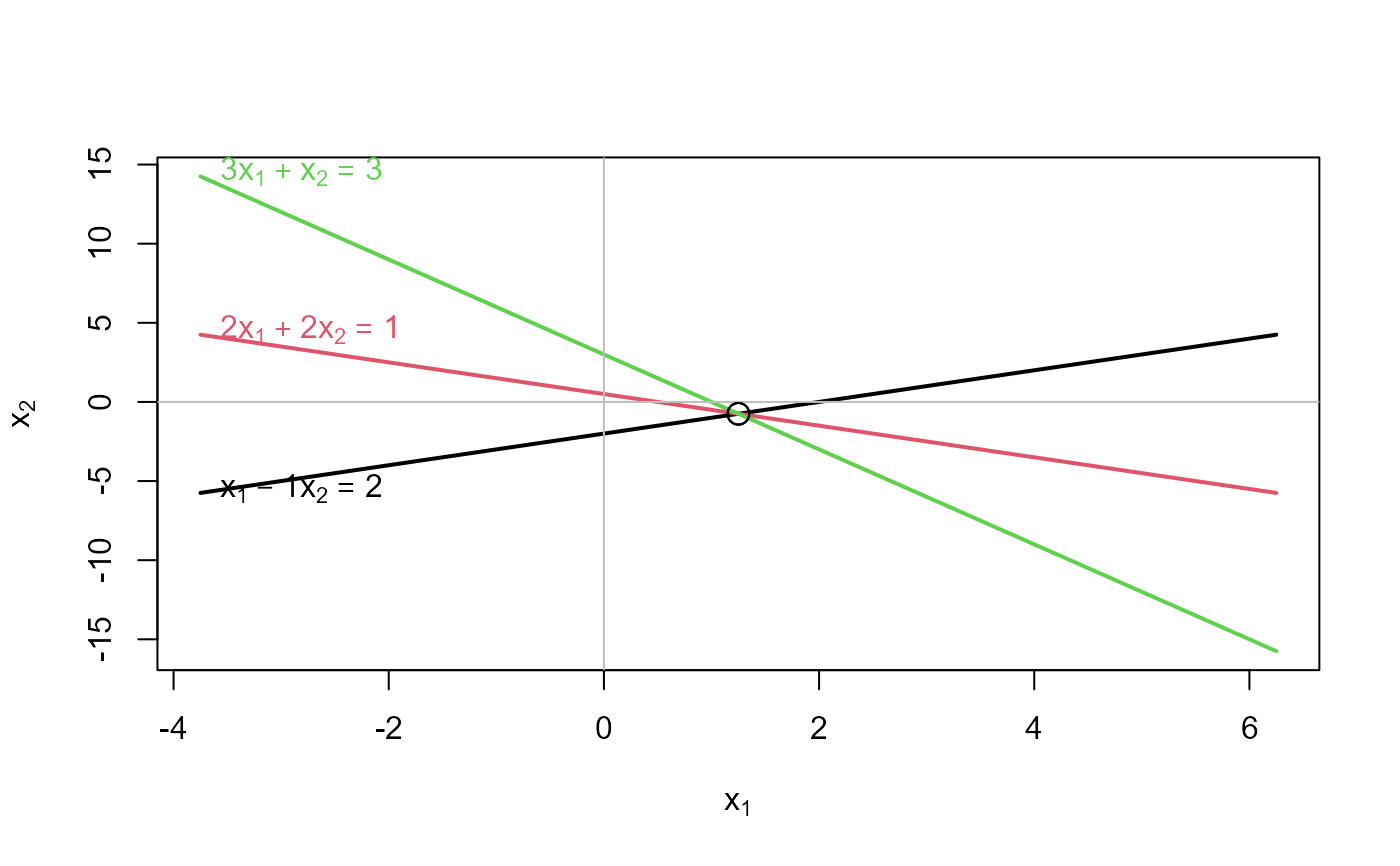
# consistent equations
A<- matrix(c(1,2,3, -1, 2, 1),3,2)
b <- c(2,1,3)
showEqn(A, b)
#> 1*x1 - 1*x2  =  2 
#> 2*x1 + 2*x2  =  1 
#> 3*x1 + 1*x2  =  3 
plotEqn(A,b)
#>   x[1] - 1*x[2]  =  2 
#> 2*x[1] + 2*x[2]  =  1 
#> 3*x[1]   + x[2]  =  3 


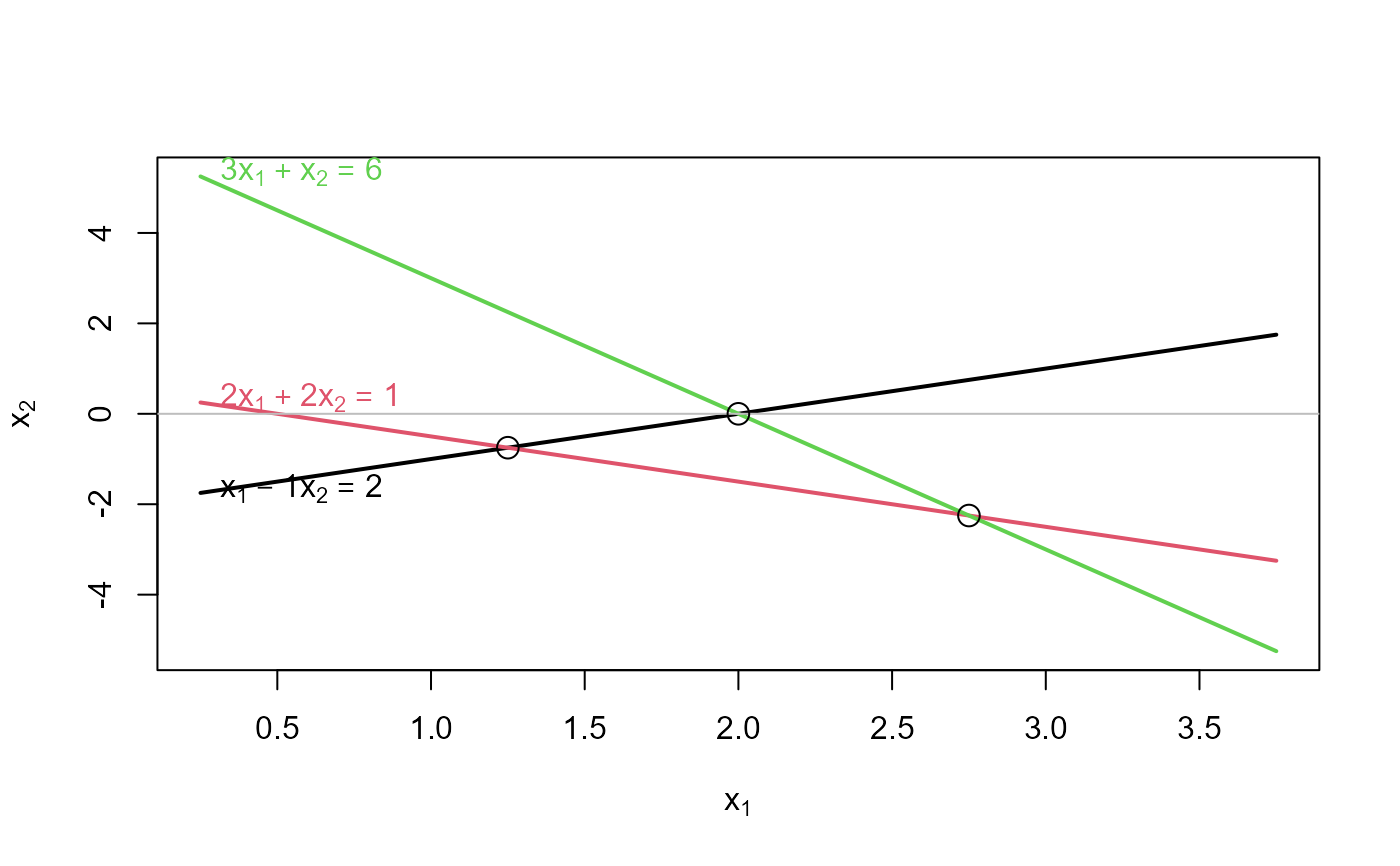
# inconsistent equations
b <- c(2,1,6)
showEqn(A, b)
#> 1*x1 - 1*x2  =  2 
#> 2*x1 + 2*x2  =  1 
#> 3*x1 + 1*x2  =  6 
plotEqn(A,b)
#>   x[1] - 1*x[2]  =  2 
#> 2*x[1] + 2*x[2]  =  1 
#> 3*x[1]   + x[2]  =  6