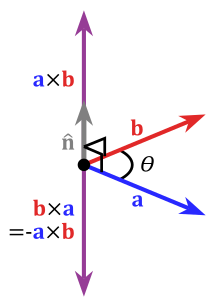
Given two linearly independent length 3 vectors **a** and **b**, the cross product, \(\mathbf{a} \times \mathbf{b}\)
(read "a cross b"), is a vector that is perpendicular to both **a** and **b**
thus normal to the plane containing them.
Arguments
- ...
N-1 linearly independent vectors of the same length, N.
Value
Returns the generalized vector cross-product, a vector of length N.
Details
A generalization of this idea applies to two or more dimensional vectors.
See: [https://en.wikipedia.org/wiki/Cross_product] for geometric and algebraic properties.
Author
Matthew Lundberg, in a [Stack Overflow post][https://stackoverflow.com/questions/36798301/r-compute-cross-product-of-vectors-physics]
Examples
xprod(1:3, 4:6)
#> [1] -3 6 -3
# This works for an dimension
xprod(c(0,1)) # 2d
#> [1] 1 0
xprod(c(1,0,0), c(0,1,0)) # 3d
#> [1] 0 0 1
xprod(c(1,1,1), c(0,1,0)) # 3d
#> [1] -1 0 1
xprod(c(1,0,0,0), c(0,1,0,0), c(0,0,1,0)) # 4d
#> [1] 0 0 0 -1