This function creates various types of “bubble” plots of influence measures with the areas of the circles representing the observations proportional to generalized Cook's distances.
Usage
# S3 method for class 'mlm'
influencePlot(
model,
scale = 12,
type = c("stres", "LR", "cookd"),
infl = mlm.influence(model, do.coef = FALSE),
FUN = det,
fill = TRUE,
fill.col = "red",
fill.alpha.max = 0.5,
labels,
id.method = "noteworthy",
id.n = if (id.method[1] == "identify") Inf else 0,
id.cex = 1,
id.col = palette()[1],
ref.col = "gray",
ref.lty = 2,
ref.lab = TRUE,
...
)Arguments
- model
An
mlmobject, as returned bylmwith a multivariate response.- scale
a factor to adjust the radii of the circles, in relation to
sqrt(CookD)- type
Type of plot: one of
c("stres", "cookd", "LR"). See Details.- infl
influence measure structure as returned by
mlm.influence- FUN
For
m>1, the function to be applied to the \(H\) and \(Q\) matrices returning a scalar value.FUN=detandFUN=trare possible choices, returning the \(|H|\) and \(tr(H)\) respectively.- fill, fill.col, fill.alpha.max
fill: logical, specifying whether the circles should be filled. Whenfill=TRUE,fill.colgives the base fill color to which transparency specified byfill.alpha.maxis applied.- labels, id.method, id.n, id.cex, id.col
settings for labeling points; see
showLabelsfor details. To omit point labeling, setid.n=0, the default. The defaultid.method="noteworthy"is used in this function to indicate setting labels for points with large Studentized residuals, hat-values or Cook's distances. See Details below. Setid.method="identify"for interactive point identification.- ref.col, ref.lty, ref.lab
arguments for reference lines. Incompletely implemented in this version
- ...
other arguments passed down
Value
If points are identified, returns a data frame with the hat values, Studentized residuals and Cook's distance of the identified points. If no points are identified, nothing is returned. This function is primarily used for its side-effect of drawing a plot.
Details
type="stres" plots squared (internally) Studentized residuals against
hat values;
type="cookd" plots Cook's distance against hat values;
type="LR" plots residual components against leverage components, with
the attractive property that contours of constant Cook's distance fall on diagonal
lines with slope = -1. Adjacent reference lines represent multiples of influence.
The id.method="noteworthy" setting also requires setting
id.n>0 to have any effect. Using id.method="noteworthy", and
id.n>0, the number of points labeled is the union of the largest
id.n values on each of L, R, and CookD.
References
Barrett, B. E. and Ling, R. F. (1992). General Classes of Influence Measures for Multivariate Regression. Journal of the American Statistical Association, 87(417), 184-191.
Barrett, B. E. (2003). Understanding Influence in Multivariate Regression Communications in Statistics - Theory and Methods, 32, 667-680.
McCulloch, C. E. & Meeter, D. (1983). Discussion of "Outliers..." by R. J. Beckman and R. D. Cook. Technometrics, 25, 152-155
See also
influencePlot in the car package
Examples
data(Rohwer, package="heplots")
Rohwer2 <- subset(Rohwer, subset=group==2)
Rohwer.mod <- lm(cbind(SAT, PPVT, Raven) ~ n+s+ns+na+ss, data=Rohwer2)
# Types of influence plots
influencePlot(Rohwer.mod, id.n=4, type="stres")
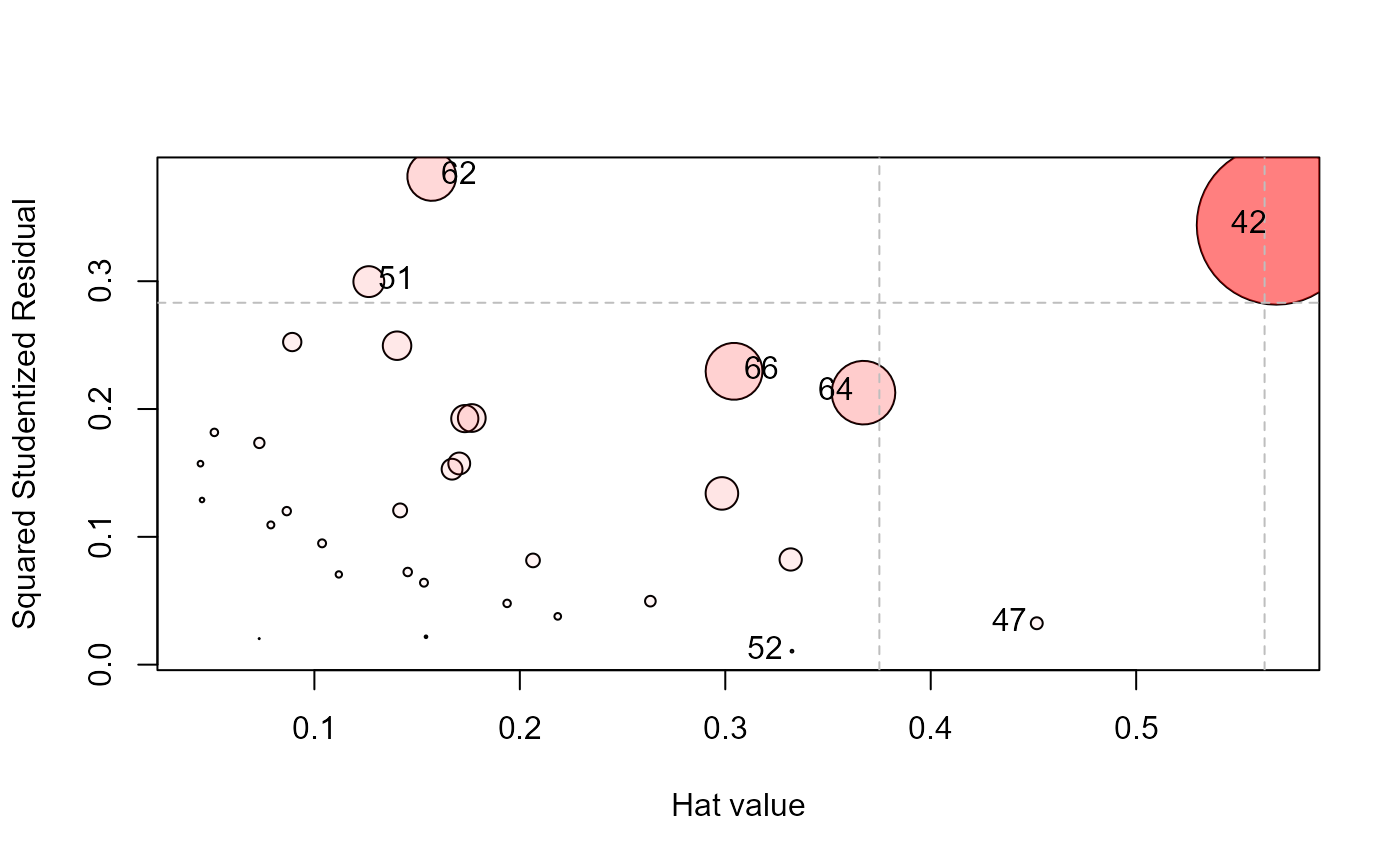 #> H Q CookD L R
#> 42 0.5682146 0.34387765 0.84671734 1.3159654 0.79640874
#> 47 0.4516115 0.03239271 0.06339198 0.8235248 0.05906890
#> 51 0.1264993 0.29967992 0.16427359 0.1448187 0.34307919
#> 52 0.3324674 0.01054411 0.01519082 0.4980543 0.01579565
#> 62 0.1571260 0.38198170 0.26008352 0.1864170 0.45318959
#> 64 0.3672647 0.21279661 0.33866160 0.5804397 0.33631219
#> 66 0.3042700 0.22949988 0.30259634 0.4373392 0.32986917
influencePlot(Rohwer.mod, id.n=4, type="LR")
#> H Q CookD L R
#> 42 0.5682146 0.34387765 0.84671734 1.3159654 0.79640874
#> 47 0.4516115 0.03239271 0.06339198 0.8235248 0.05906890
#> 51 0.1264993 0.29967992 0.16427359 0.1448187 0.34307919
#> 52 0.3324674 0.01054411 0.01519082 0.4980543 0.01579565
#> 62 0.1571260 0.38198170 0.26008352 0.1864170 0.45318959
#> 64 0.3672647 0.21279661 0.33866160 0.5804397 0.33631219
#> 66 0.3042700 0.22949988 0.30259634 0.4373392 0.32986917
influencePlot(Rohwer.mod, id.n=4, type="LR")
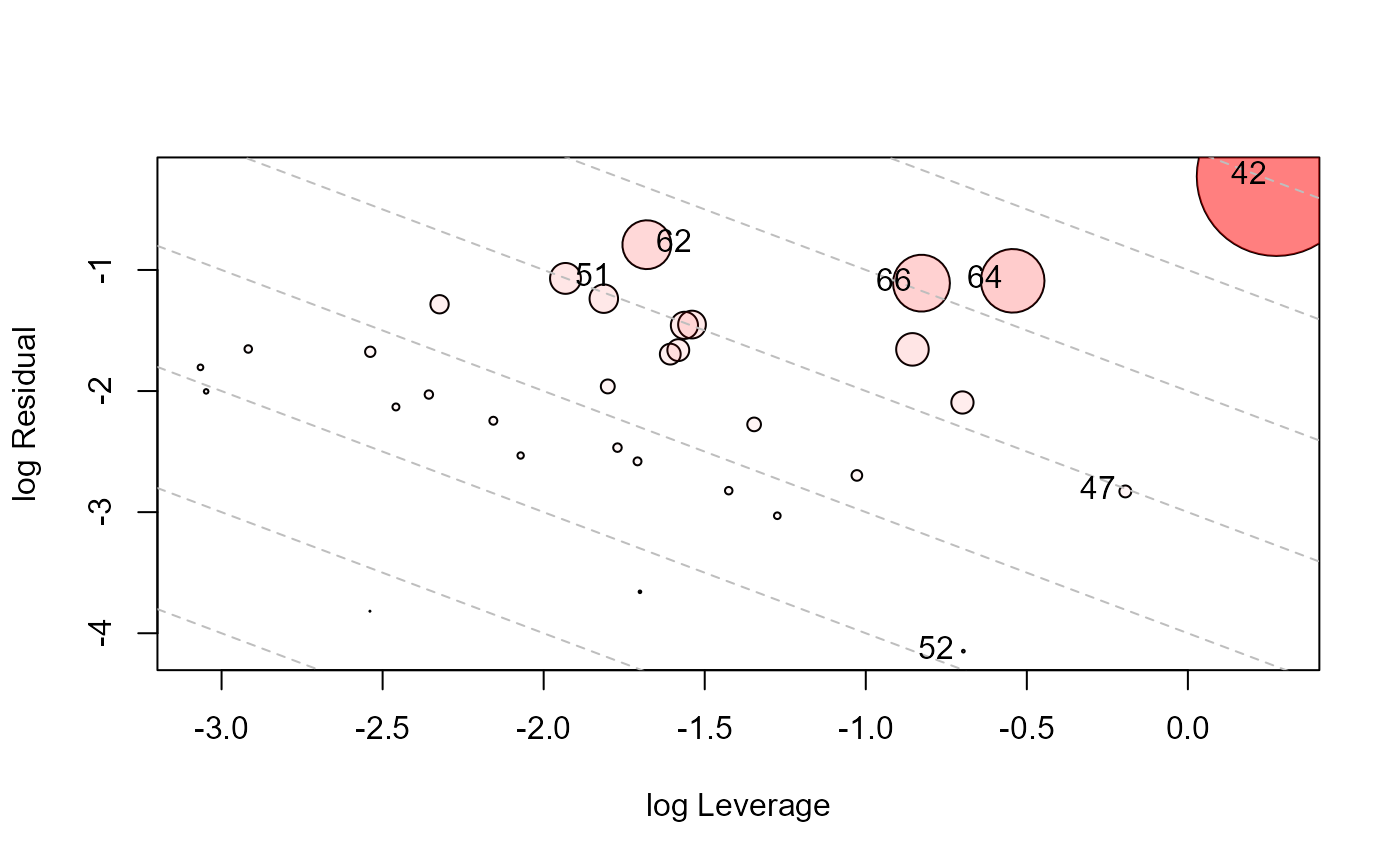 #> H Q CookD L R
#> 42 0.5682146 0.34387765 0.84671734 1.3159654 0.79640874
#> 47 0.4516115 0.03239271 0.06339198 0.8235248 0.05906890
#> 51 0.1264993 0.29967992 0.16427359 0.1448187 0.34307919
#> 52 0.3324674 0.01054411 0.01519082 0.4980543 0.01579565
#> 62 0.1571260 0.38198170 0.26008352 0.1864170 0.45318959
#> 64 0.3672647 0.21279661 0.33866160 0.5804397 0.33631219
#> 66 0.3042700 0.22949988 0.30259634 0.4373392 0.32986917
influencePlot(Rohwer.mod, id.n=4, type="cookd")
#> H Q CookD L R
#> 42 0.5682146 0.34387765 0.84671734 1.3159654 0.79640874
#> 47 0.4516115 0.03239271 0.06339198 0.8235248 0.05906890
#> 51 0.1264993 0.29967992 0.16427359 0.1448187 0.34307919
#> 52 0.3324674 0.01054411 0.01519082 0.4980543 0.01579565
#> 62 0.1571260 0.38198170 0.26008352 0.1864170 0.45318959
#> 64 0.3672647 0.21279661 0.33866160 0.5804397 0.33631219
#> 66 0.3042700 0.22949988 0.30259634 0.4373392 0.32986917
influencePlot(Rohwer.mod, id.n=4, type="cookd")
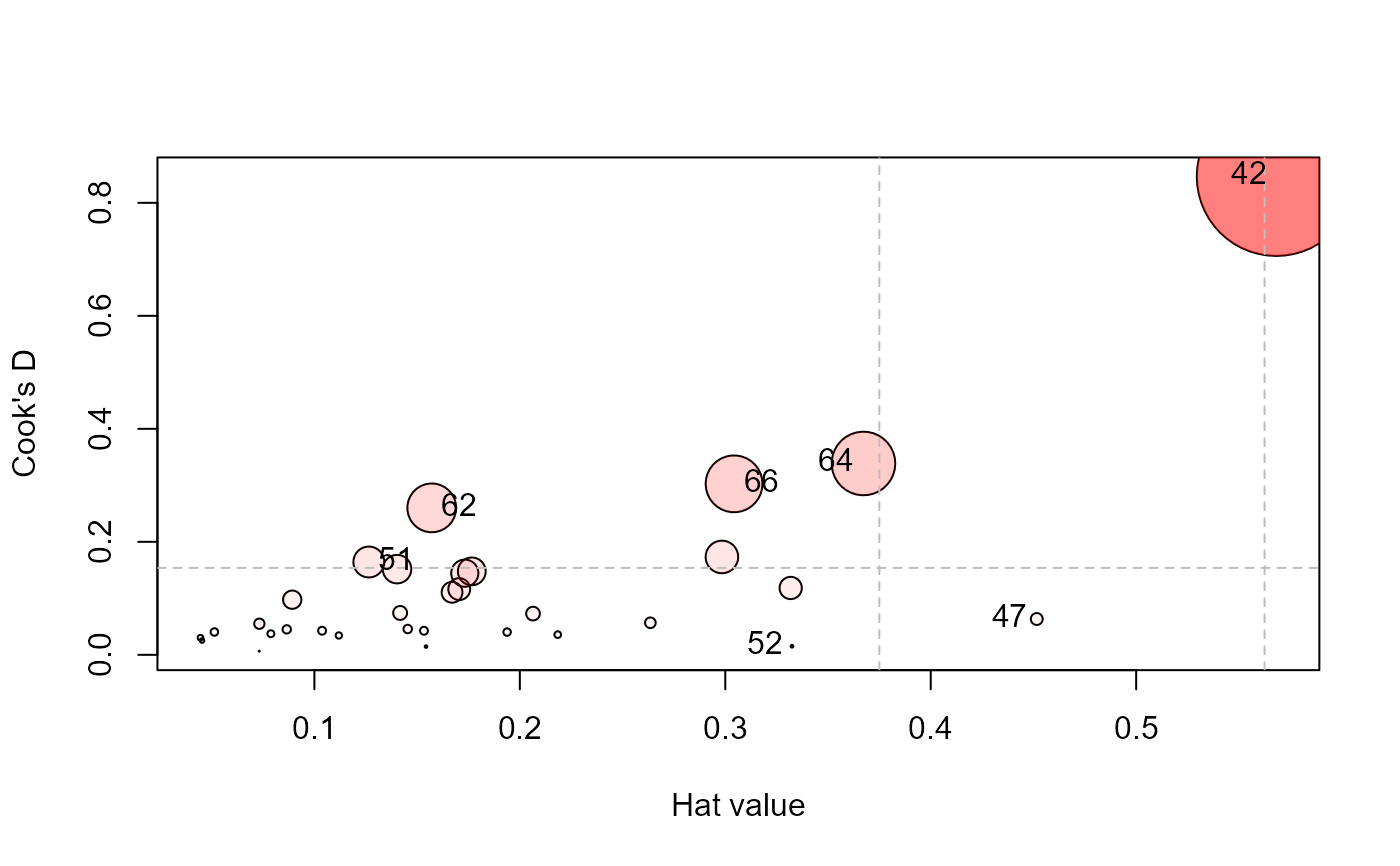 #> H Q CookD L R
#> 42 0.5682146 0.34387765 0.84671734 1.3159654 0.79640874
#> 47 0.4516115 0.03239271 0.06339198 0.8235248 0.05906890
#> 51 0.1264993 0.29967992 0.16427359 0.1448187 0.34307919
#> 52 0.3324674 0.01054411 0.01519082 0.4980543 0.01579565
#> 62 0.1571260 0.38198170 0.26008352 0.1864170 0.45318959
#> 64 0.3672647 0.21279661 0.33866160 0.5804397 0.33631219
#> 66 0.3042700 0.22949988 0.30259634 0.4373392 0.32986917
# Sake data
data(Sake, package="heplots")
Sake.mod <- lm(cbind(taste,smell) ~ ., data=Sake)
influencePlot(Sake.mod, id.n=3, type="stres")
#> H Q CookD L R
#> 42 0.5682146 0.34387765 0.84671734 1.3159654 0.79640874
#> 47 0.4516115 0.03239271 0.06339198 0.8235248 0.05906890
#> 51 0.1264993 0.29967992 0.16427359 0.1448187 0.34307919
#> 52 0.3324674 0.01054411 0.01519082 0.4980543 0.01579565
#> 62 0.1571260 0.38198170 0.26008352 0.1864170 0.45318959
#> 64 0.3672647 0.21279661 0.33866160 0.5804397 0.33631219
#> 66 0.3042700 0.22949988 0.30259634 0.4373392 0.32986917
# Sake data
data(Sake, package="heplots")
Sake.mod <- lm(cbind(taste,smell) ~ ., data=Sake)
influencePlot(Sake.mod, id.n=3, type="stres")
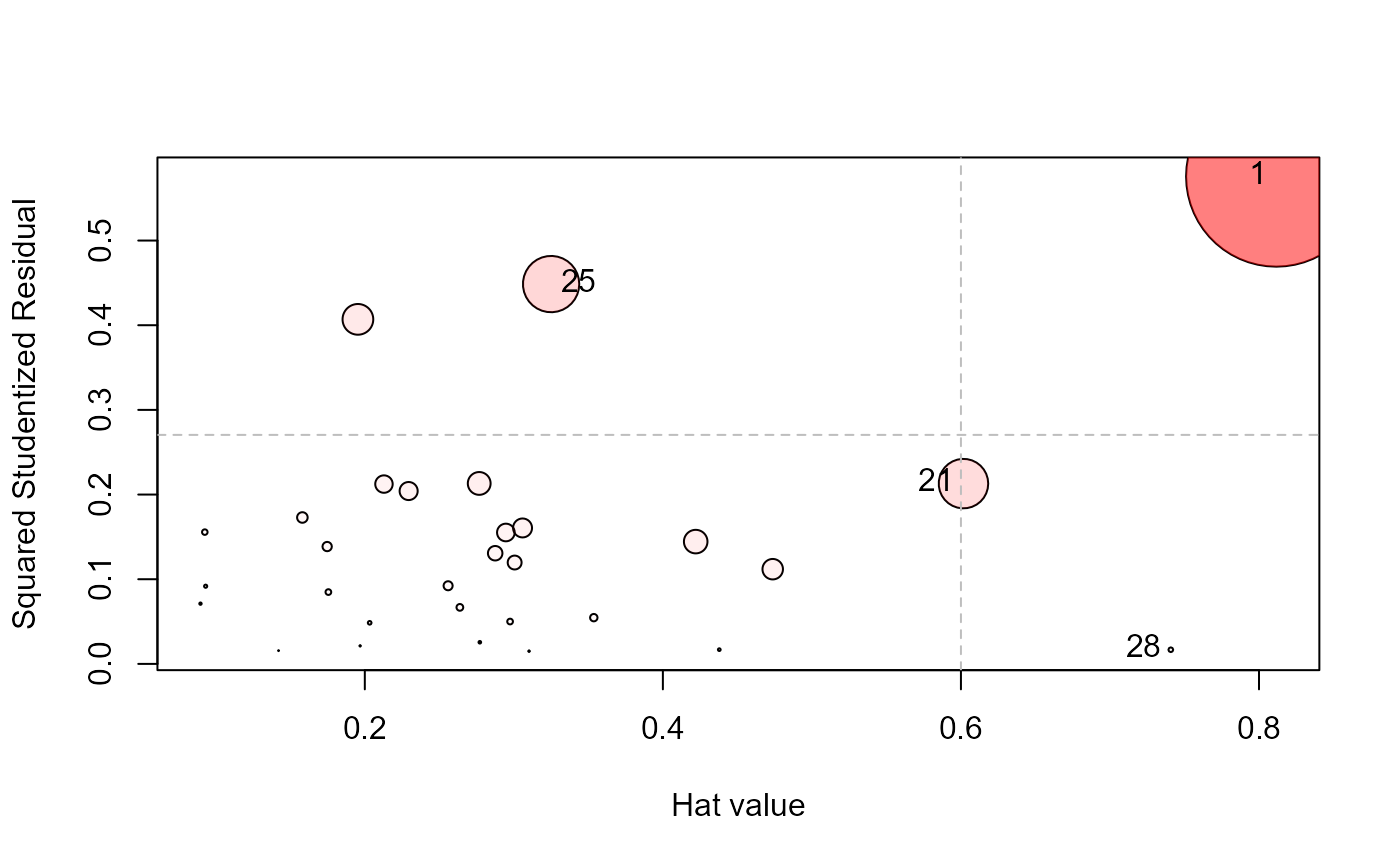 #> H Q CookD L R
#> 1 0.8116280 0.57573451 1.09032522 4.3086442 3.05636964
#> 21 0.6017041 0.21291909 0.29893332 1.5106959 0.53457509
#> 25 0.3250006 0.44858236 0.34017563 0.4814829 0.66456709
#> 28 0.7408215 0.01671372 0.02889105 2.8583448 0.06448728
influencePlot(Sake.mod, id.n=3, type="LR")
#> H Q CookD L R
#> 1 0.8116280 0.57573451 1.09032522 4.3086442 3.05636964
#> 21 0.6017041 0.21291909 0.29893332 1.5106959 0.53457509
#> 25 0.3250006 0.44858236 0.34017563 0.4814829 0.66456709
#> 28 0.7408215 0.01671372 0.02889105 2.8583448 0.06448728
influencePlot(Sake.mod, id.n=3, type="LR")
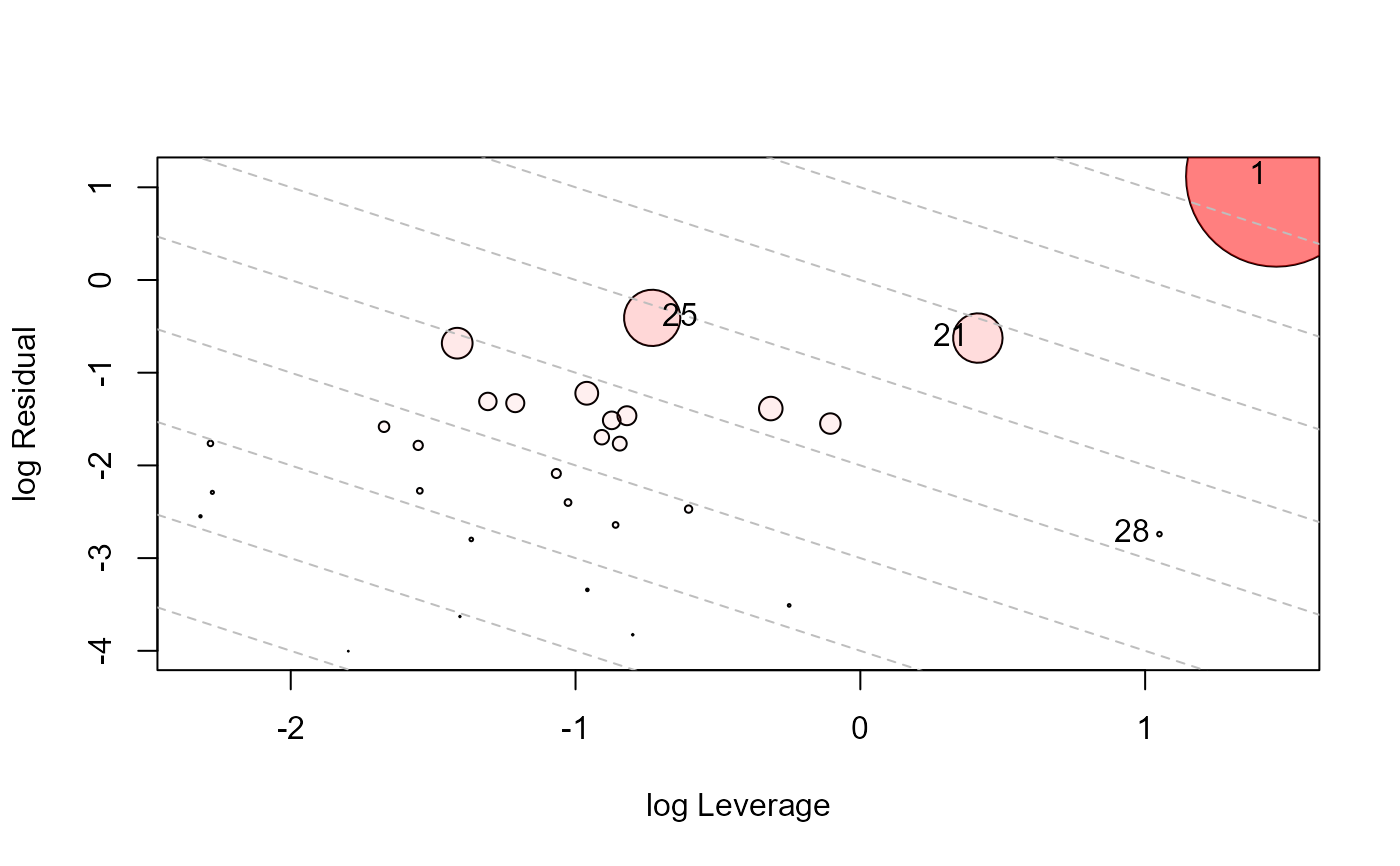 #> H Q CookD L R
#> 1 0.8116280 0.57573451 1.09032522 4.3086442 3.05636964
#> 21 0.6017041 0.21291909 0.29893332 1.5106959 0.53457509
#> 25 0.3250006 0.44858236 0.34017563 0.4814829 0.66456709
#> 28 0.7408215 0.01671372 0.02889105 2.8583448 0.06448728
influencePlot(Sake.mod, id.n=3, type="cookd")
#> H Q CookD L R
#> 1 0.8116280 0.57573451 1.09032522 4.3086442 3.05636964
#> 21 0.6017041 0.21291909 0.29893332 1.5106959 0.53457509
#> 25 0.3250006 0.44858236 0.34017563 0.4814829 0.66456709
#> 28 0.7408215 0.01671372 0.02889105 2.8583448 0.06448728
influencePlot(Sake.mod, id.n=3, type="cookd")
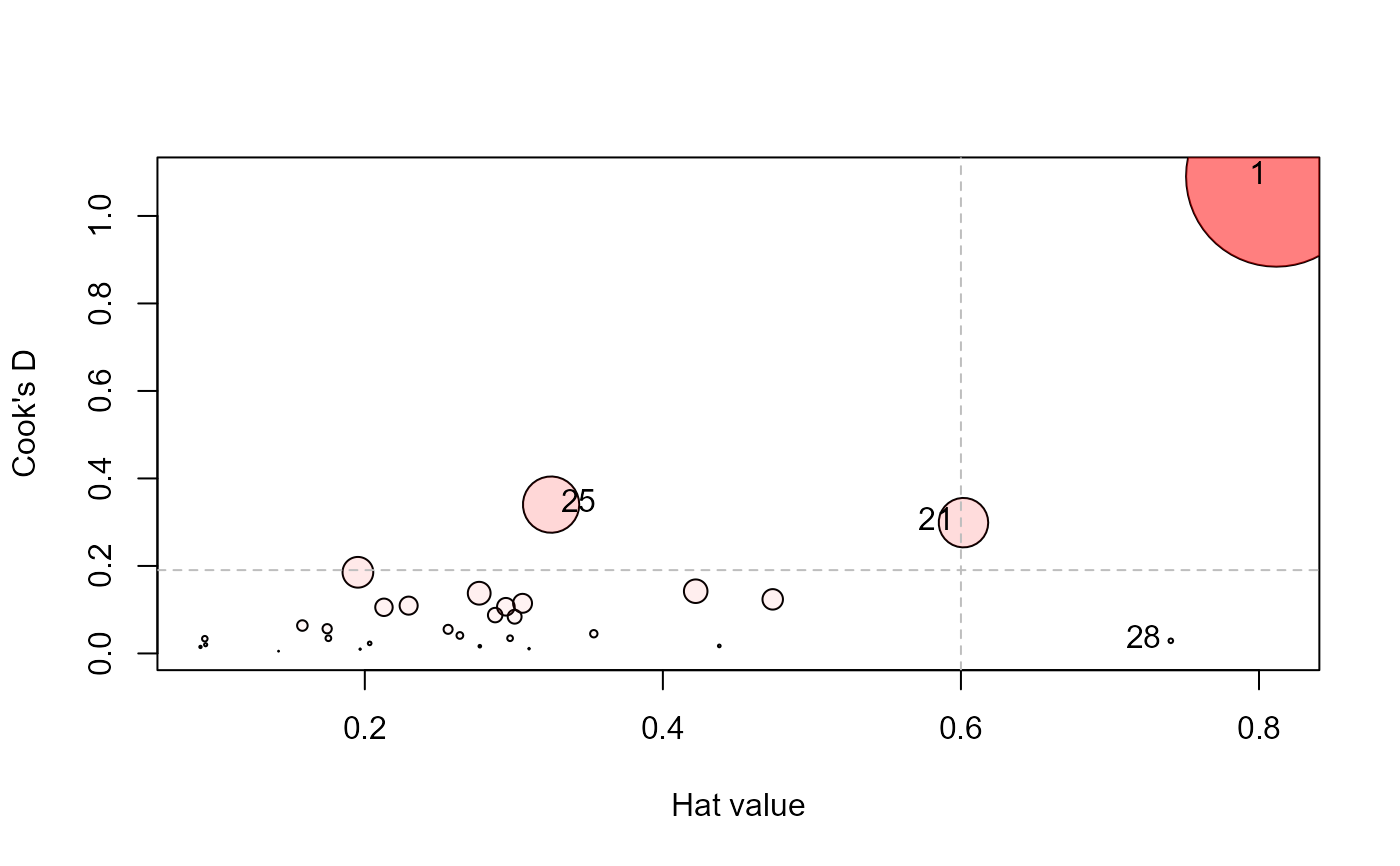 #> H Q CookD L R
#> 1 0.8116280 0.57573451 1.09032522 4.3086442 3.05636964
#> 21 0.6017041 0.21291909 0.29893332 1.5106959 0.53457509
#> 25 0.3250006 0.44858236 0.34017563 0.4814829 0.66456709
#> 28 0.7408215 0.01671372 0.02889105 2.8583448 0.06448728
# Adopted data
data(Adopted, package="heplots")
Adopted.mod <- lm(cbind(Age2IQ, Age4IQ, Age8IQ, Age13IQ) ~ AMED + BMIQ, data=Adopted)
influencePlot(Adopted.mod, id.n=3)
#> H Q CookD L R
#> 1 0.8116280 0.57573451 1.09032522 4.3086442 3.05636964
#> 21 0.6017041 0.21291909 0.29893332 1.5106959 0.53457509
#> 25 0.3250006 0.44858236 0.34017563 0.4814829 0.66456709
#> 28 0.7408215 0.01671372 0.02889105 2.8583448 0.06448728
# Adopted data
data(Adopted, package="heplots")
Adopted.mod <- lm(cbind(Age2IQ, Age4IQ, Age8IQ, Age13IQ) ~ AMED + BMIQ, data=Adopted)
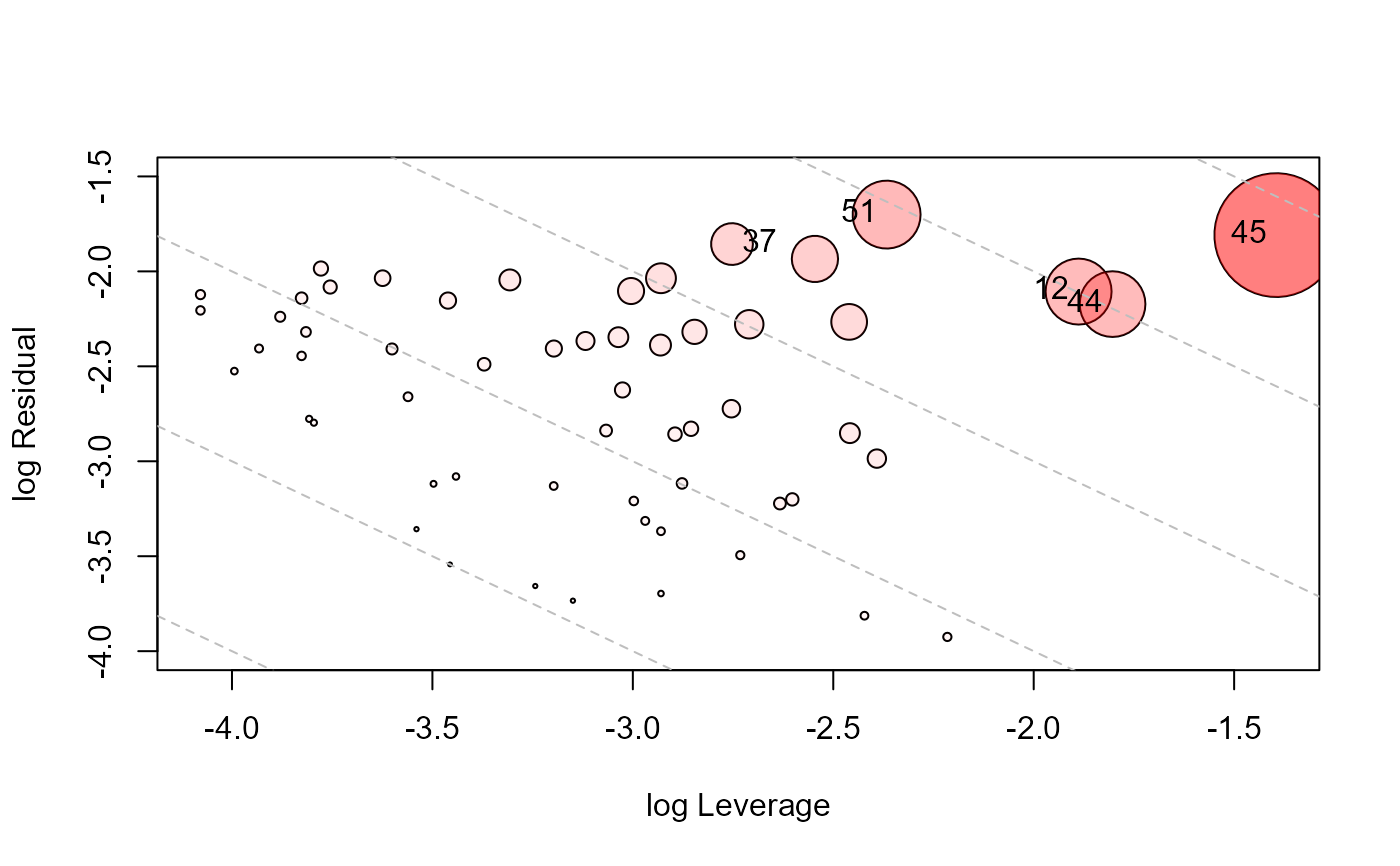
influencePlot(Adopted.mod, id.n=3)
 #> H Q CookD L R
#> 12 0.13146834 0.10567954 0.2732391 0.15136851 0.1216761
#> 37 0.05993805 0.14690519 0.1731692 0.06375968 0.1562718
#> 44 0.14144842 0.09779596 0.2720507 0.16475239 0.1139081
#> 45 0.19864788 0.13127108 0.5128422 0.24789088 0.1638120
#> 51 0.08572766 0.16685333 0.2813109 0.09376600 0.1824985
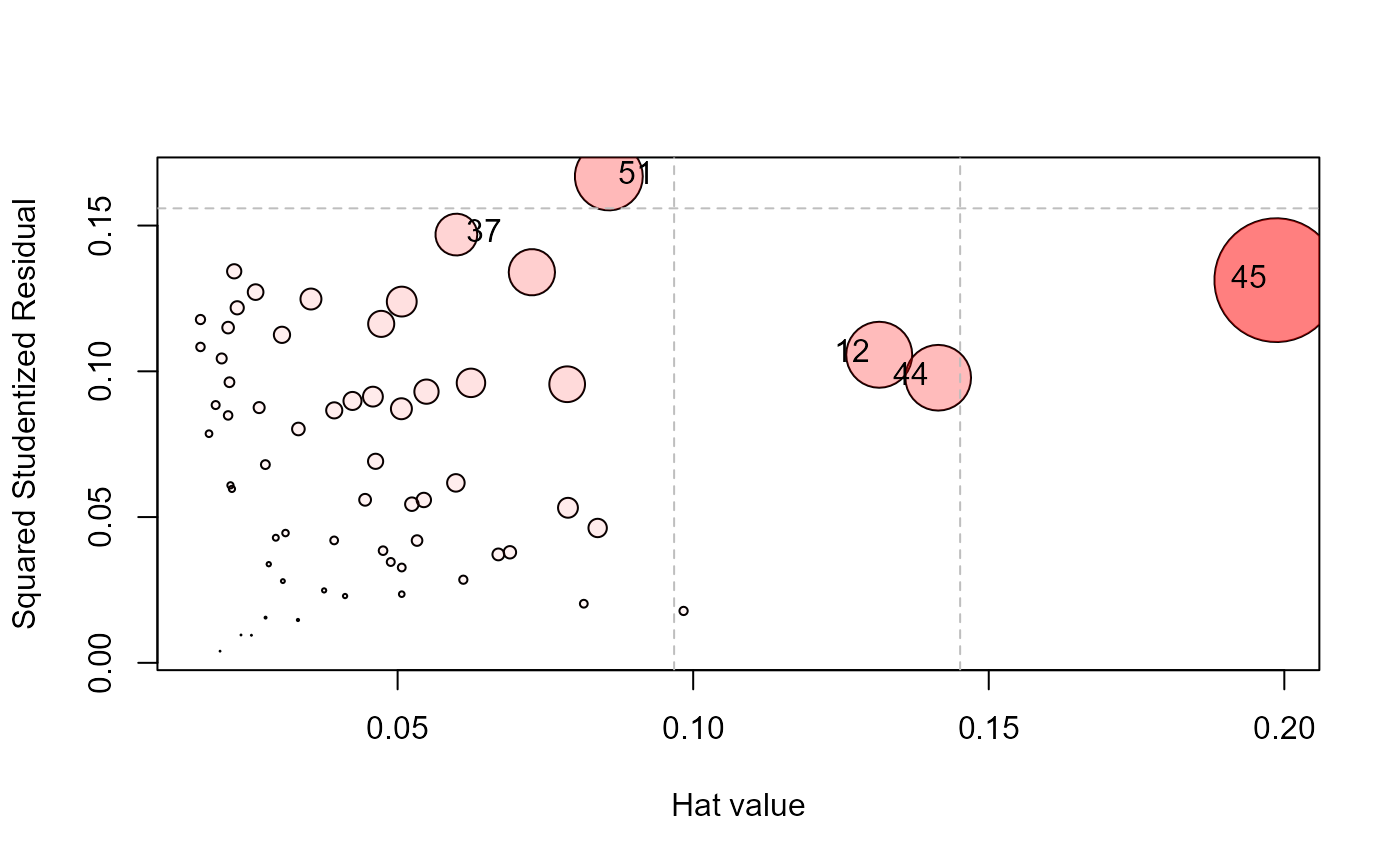
influencePlot(Adopted.mod, id.n=3, type="LR", ylim=c(-4,-1.5))
#> H Q CookD L R
#> 12 0.13146834 0.10567954 0.2732391 0.15136851 0.1216761
#> 37 0.05993805 0.14690519 0.1731692 0.06375968 0.1562718
#> 44 0.14144842 0.09779596 0.2720507 0.16475239 0.1139081
#> 45 0.19864788 0.13127108 0.5128422 0.24789088 0.1638120
#> 51 0.08572766 0.16685333 0.2813109 0.09376600 0.1824985
influencePlot(Adopted.mod, id.n=3, type="LR", ylim=c(-4,-1.5))
 #> H Q CookD L R
#> 12 0.13146834 0.10567954 0.2732391 0.15136851 0.1216761
#> 37 0.05993805 0.14690519 0.1731692 0.06375968 0.1562718
#> 44 0.14144842 0.09779596 0.2720507 0.16475239 0.1139081
#> 45 0.19864788 0.13127108 0.5128422 0.24789088 0.1638120
#> 51 0.08572766 0.16685333 0.2813109 0.09376600 0.1824985
# schooldata
data(schooldata, package = "heplots")
school.mod <- lm(cbind(reading, mathematics, selfesteem) ~ .,
data=schooldata)
influencePlot(school.mod, id.n=4, type="stres")
#> H Q CookD L R
#> 12 0.13146834 0.10567954 0.2732391 0.15136851 0.1216761
#> 37 0.05993805 0.14690519 0.1731692 0.06375968 0.1562718
#> 44 0.14144842 0.09779596 0.2720507 0.16475239 0.1139081
#> 45 0.19864788 0.13127108 0.5128422 0.24789088 0.1638120
#> 51 0.08572766 0.16685333 0.2813109 0.09376600 0.1824985
# schooldata
data(schooldata, package = "heplots")
school.mod <- lm(cbind(reading, mathematics, selfesteem) ~ .,
data=schooldata)
influencePlot(school.mod, id.n=4, type="stres")
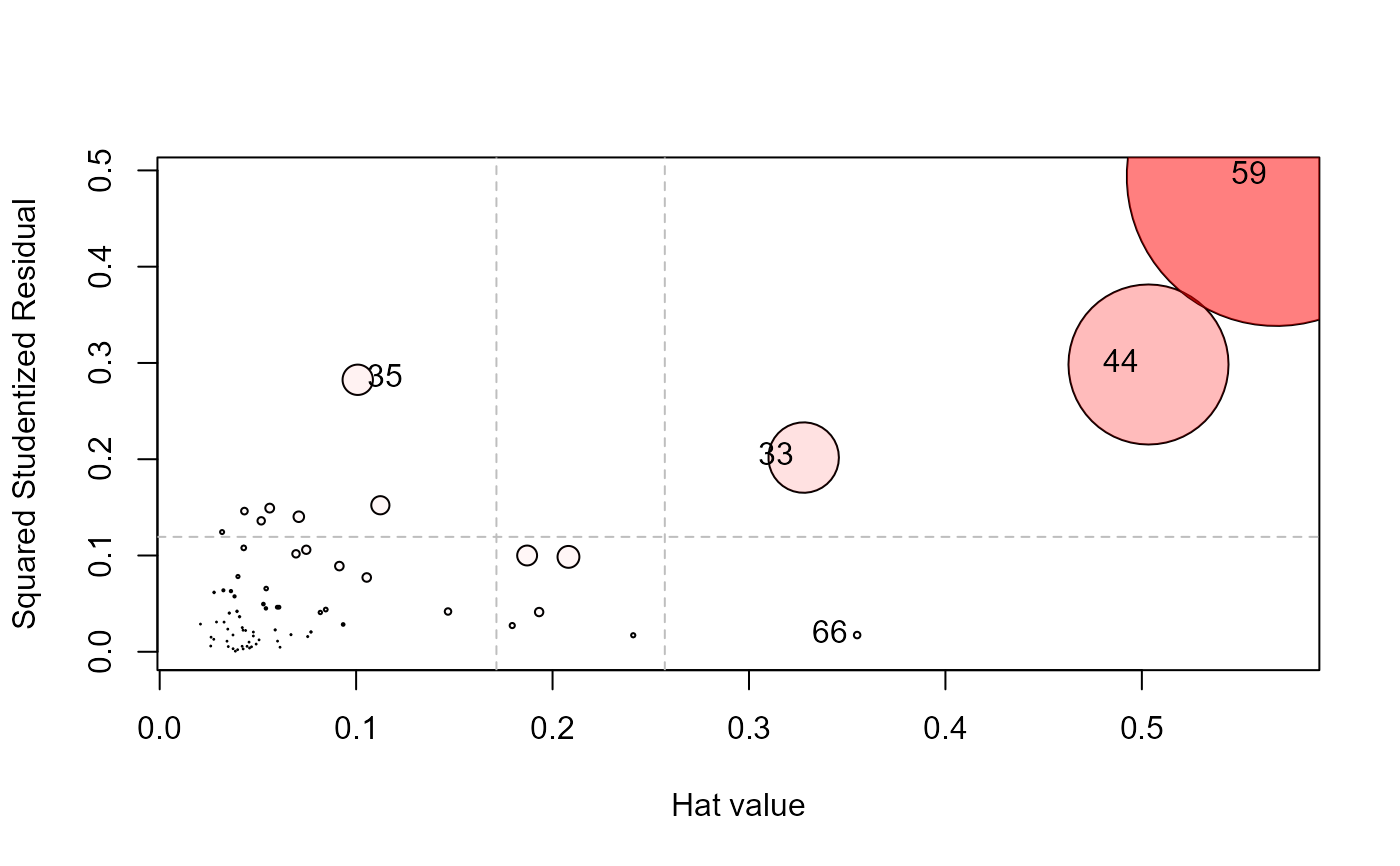 #> H Q CookD L R
#> 33 0.3278356 0.20171727 0.70538781 0.4877313 0.30010110
#> 35 0.1008230 0.28251745 0.30383220 0.1121281 0.31419561
#> 44 0.5033777 0.29839975 1.60221616 1.0136025 0.60085848
#> 59 0.5684534 0.49374467 2.99382203 1.3172466 1.14412817
#> 66 0.3550542 0.01735437 0.06572524 0.5505179 0.02690826
influencePlot(school.mod, id.n=4, type="LR")
#> H Q CookD L R
#> 33 0.3278356 0.20171727 0.70538781 0.4877313 0.30010110
#> 35 0.1008230 0.28251745 0.30383220 0.1121281 0.31419561
#> 44 0.5033777 0.29839975 1.60221616 1.0136025 0.60085848
#> 59 0.5684534 0.49374467 2.99382203 1.3172466 1.14412817
#> 66 0.3550542 0.01735437 0.06572524 0.5505179 0.02690826
influencePlot(school.mod, id.n=4, type="LR")
 #> H Q CookD L R
#> 33 0.3278356 0.20171727 0.70538781 0.4877313 0.30010110
#> 35 0.1008230 0.28251745 0.30383220 0.1121281 0.31419561
#> 44 0.5033777 0.29839975 1.60221616 1.0136025 0.60085848
#> 59 0.5684534 0.49374467 2.99382203 1.3172466 1.14412817
#> 66 0.3550542 0.01735437 0.06572524 0.5505179 0.02690826
#> H Q CookD L R
#> 33 0.3278356 0.20171727 0.70538781 0.4877313 0.30010110
#> 35 0.1008230 0.28251745 0.30383220 0.1121281 0.31419561
#> 44 0.5033777 0.29839975 1.60221616 1.0136025 0.60085848
#> 59 0.5684534 0.49374467 2.99382203 1.3172466 1.14412817
#> 66 0.3550542 0.01735437 0.06572524 0.5505179 0.02690826
