In an experiment to investigate the effect of cutting length (two levels) and planting time (two levels) on the survival of plum root cuttings, 240 cuttings were planted for each of the 2 x 2 combinations of these factors, and their survival was later recorded.
Format
A 3-dimensional array resulting from cross-tabulating 3 variables for 960 observations. The variable names and their levels are:
| dim | Name | Levels |
| 1 | Alive | "Alive", "Dead" |
| 2 | Time | "Now", "Spring" |
| 3 | Length | "Long", "Short" |
Source
Hand, D. and Daly, F. and Lunn, A. D.and McConway, K. J. and Ostrowski, E. (1994). A Handbook of Small Data Sets. London: Chapman & Hall, p. 15, # 19.
Details
Bartlett (1935) used these data to illustrate a method for testing for no three-way interaction in a contingency table.
References
Bartlett, M. S. (1935). Contingency Table Interactions Journal of the Royal Statistical Society, Supplement, 1935, 2, 248-252.
Examples
data(Bartlett)
# measures of association
assocstats(Bartlett)
#> $`Length:Long`
#> X^2 df P(> X^2)
#> Likelihood Ratio 43.873 1 3.5048e-11
#> Pearson 43.200 1 4.9421e-11
#>
#> Phi-Coefficient : 0.3
#> Contingency Coeff.: 0.287
#> Cramer's V : 0.3
#>
#> $`Length:Short`
#> X^2 df P(> X^2)
#> Likelihood Ratio 61.310 1 4.8850e-15
#> Pearson 58.744 1 1.7986e-14
#>
#> Phi-Coefficient : 0.35
#> Contingency Coeff.: 0.33
#> Cramer's V : 0.35
#>
oddsratio(Bartlett)
#> log odds ratios for Alive and Time by Length
#>
#> Long Short
#> 1.238078 1.690827
# Test models
## Independence
MASS::loglm(formula = ~Alive + Time + Length, data = Bartlett)
#> Call:
#> MASS::loglm(formula = ~Alive + Time + Length, data = Bartlett)
#>
#> Statistics:
#> X^2 df P(> X^2)
#> Likelihood Ratio 151.0193 4 0
#> Pearson 141.0527 4 0
## No three-way association
MASS::loglm(formula = ~(Alive + Time + Length)^2, data = Bartlett)
#> Call:
#> MASS::loglm(formula = ~(Alive + Time + Length)^2, data = Bartlett)
#>
#> Statistics:
#> X^2 df P(> X^2)
#> Likelihood Ratio 2.293841 1 0.1298882
#> Pearson 2.270373 1 0.1318681
# Use woolf_test() for a formal test of homogeneity of odds ratios
vcd::woolf_test(Bartlett)
#>
#> Woolf-test on Homogeneity of Odds Ratios (no 3-Way assoc.)
#>
#> data: Bartlett
#> X-squared = 2.264, df = 1, p-value = 0.1324
#>
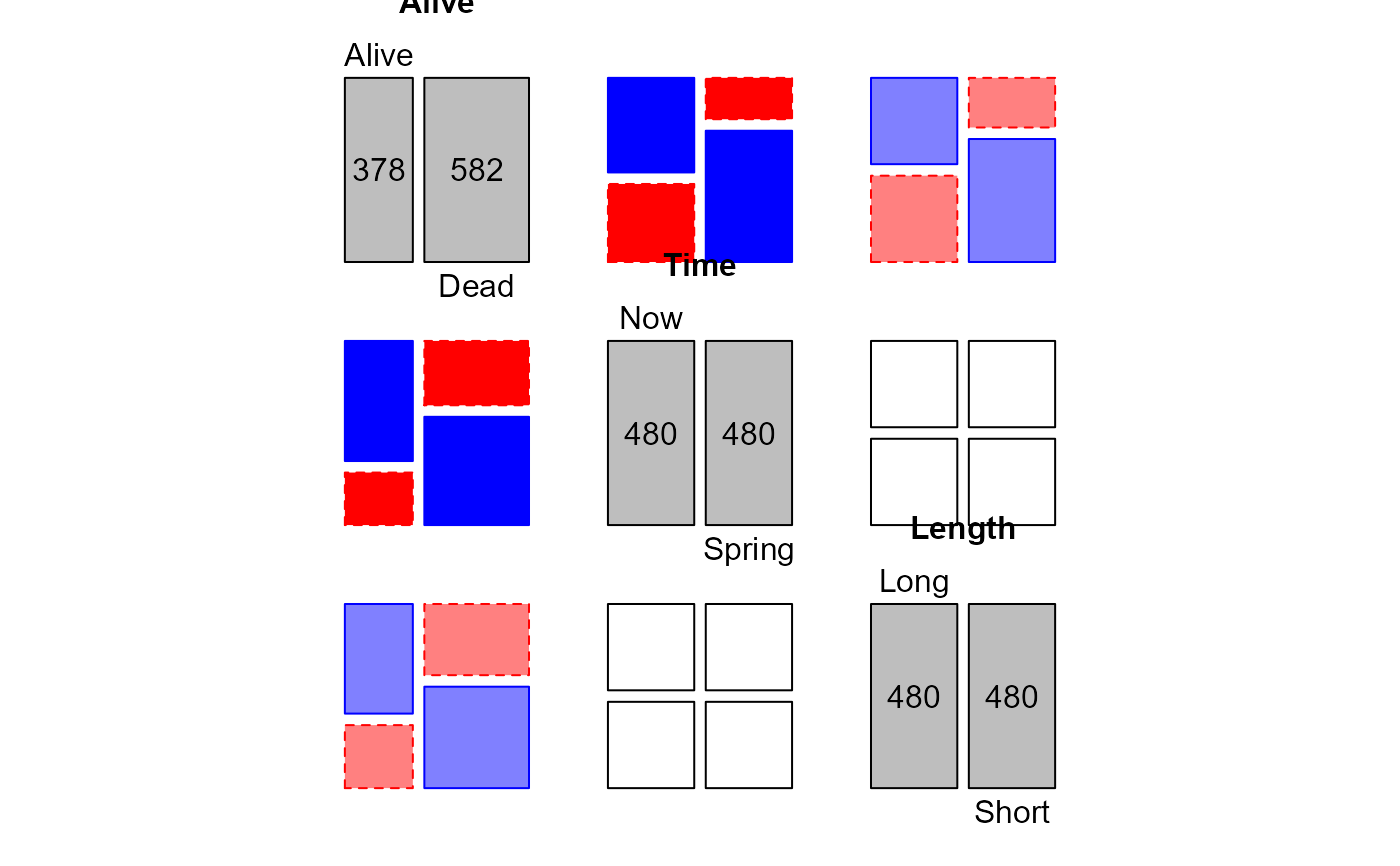
# Plots
fourfold(Bartlett, mfrow=c(1,2))
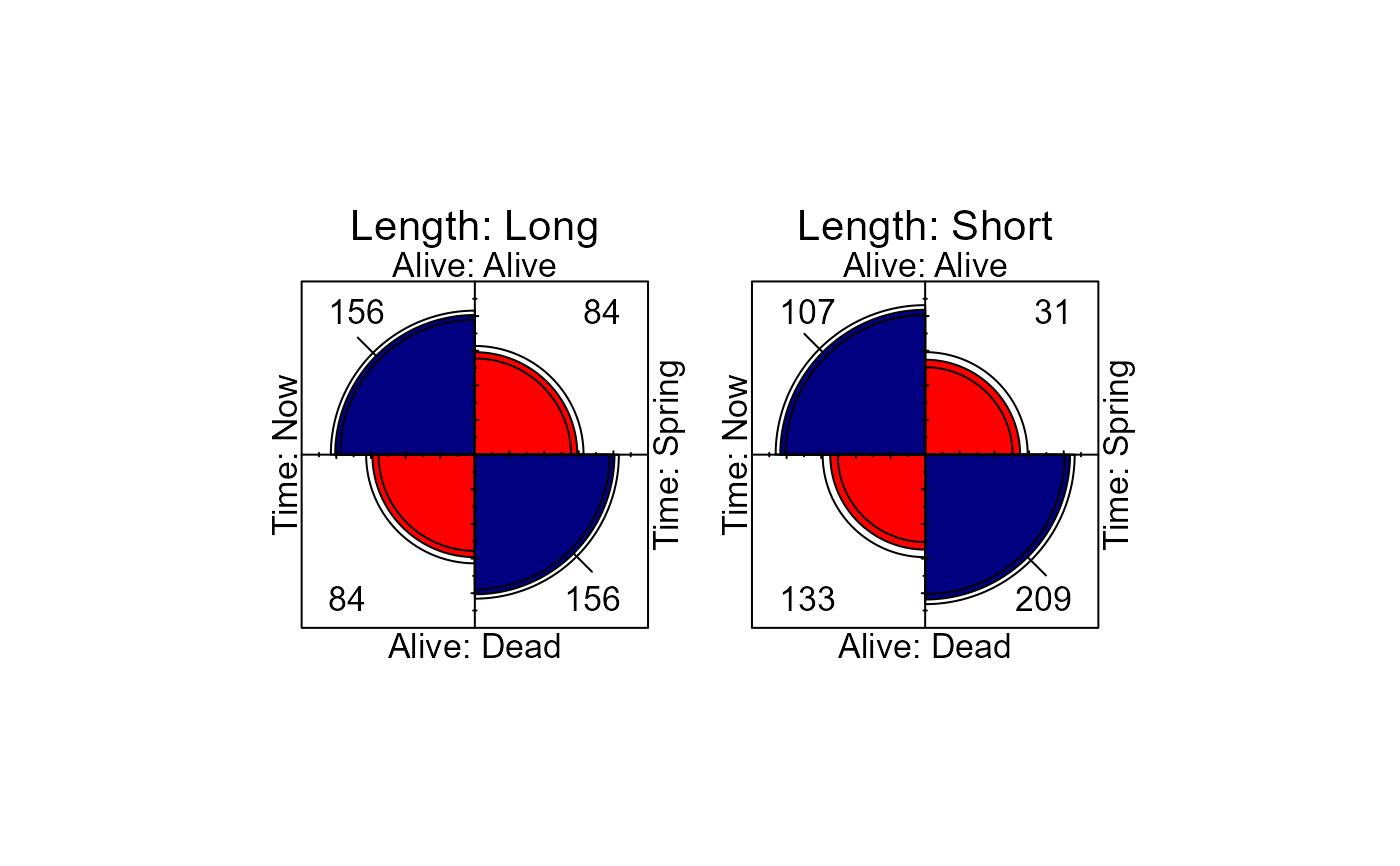mosaic(Bartlett, shade=TRUE)
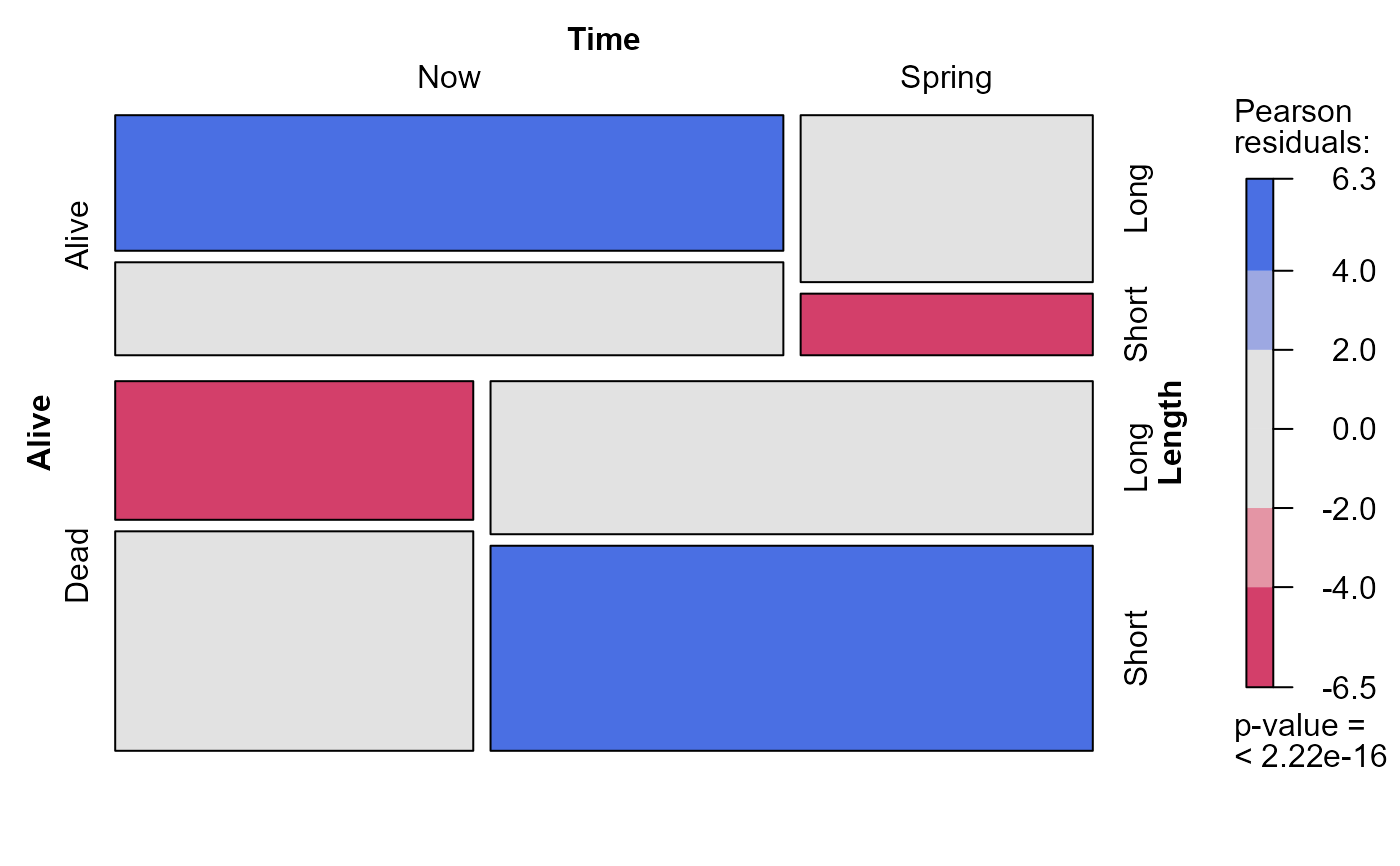pairs(Bartlett, gp=shading_Friendly)
