ICU data set — ICU • vcdExtra

The ICU data set consists of a sample of 200 subjects who were part of a much larger study on survival of patients following admission to an adult intensive care unit (ICU), derived from Hosmer, Lemeshow and Sturdivant (2013) and Friendly (2000).

The major goal of this study was to develop a logistic regression model to predict the probability of survival to hospital discharge of these patients and to study the risk factors associated with ICU mortality. The clinical details of the study are described in Lemeshow, Teres, Avrunin, and Pastides (1988).

This data set is often used to illustrate model selection methods for logistic regression.

Usage

data(ICU)

Format

A data frame with 200 observations on the following 22 variables.

died: Died before discharge?, a factor with levels No Yes
age: Patient age, a numeric vector
sex: Patient sex, a factor with levels Female Male
race: Patient race, a factor with levels Black Other White. Also represented here as white.
service: Service at ICU Admission, a factor with levels Medical Surgical
cancer: Cancer part of present problem?, a factor with levels No Yes
renal: History of chronic renal failure?, a factor with levels No Yes
infect: Infection probable at ICU admission?, a factor with levels No Yes
cpr: Patient received CPR prior to ICU admission?, a factor with levels No Yes
systolic: Systolic blood pressure at admission (mm Hg), a numeric vector
hrtrate: Heart rate at ICU Admission (beats/min), a numeric vector
previcu: Previous admission to an ICU within 6 Months?, a factor with levels No Yes
admit: Type of admission, a factor with levels Elective Emergency
fracture: Admission with a long bone, multiple, neck, single area, or hip fracture? a factor with levels No Yes
po2: PO2 from initial blood gases, a factor with levels >60 <=60
ph: pH from initial blood gases, a factor with levels >=7.25 <7.25
pco: PCO2 from initial blood gases, a factor with levels <=45 >45
bic: Bicarbonate (HCO3) level from initial blood gases, a factor with levels >=18 <18
creatin: Creatinine, from initial blood gases, a factor with levels <=2 >2
coma: Level of unconsciousness at admission to ICU, a factor with levels None Stupor Coma
white: a recoding of race, a factor with levels White Non-white
uncons: a recoding of coma a factor with levels No Yes

Details

Patient ID numbers are the rownames of the data frame.

Note that the last two variables white and uncons are a recoding of respectively race and coma to binary variables.

Source

M. Friendly (2000), Visualizing Categorical Data, Appendix B.4. SAS Institute, Cary, NC.

Hosmer, D. W. Jr., Lemeshow, S. and Sturdivant, R. X. (2013) Applied Logistic Regression, NY: Wiley, Third Edition.

References

Lemeshow, S., Teres, D., Avrunin, J. S., Pastides, H. (1988). Predicting the Outcome of Intensive Care Unit Patients. Journal of the American Statistical Association, 83, 348-356.

Examples

data(ICU)
# remove redundant variables (race, coma)
ICU1 <- ICU[,-c(4,20)]

# fit full model
icu.full <- glm(died ~ ., data=ICU1, family=binomial)
summary(icu.full)
#> 
#> Call:
#> glm(formula = died ~ ., family = binomial, data = ICU1)
#> 
#> Coefficients:
#>                  Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)     -6.726704   2.385512  -2.820  0.00481 ** 
#> age              0.056393   0.018624   3.028  0.00246 ** 
#> sexMale          0.639725   0.531393   1.204  0.22864    
#> serviceSurgical -0.673522   0.601902  -1.119  0.26315    
#> cancerYes        3.107051   1.045846   2.971  0.00297 ** 
#> renalYes        -0.035708   0.801647  -0.045  0.96447    
#> infectYes       -0.204933   0.553191  -0.370  0.71104    
#> cprYes           1.053483   1.006614   1.047  0.29530    
#> systolic        -0.015472   0.008497  -1.821  0.06864 .  
#> hrtrate         -0.002769   0.009607  -0.288  0.77317    
#> previcuYes       1.131942   0.671450   1.686  0.09183 .  
#> admitEmergency   3.079583   1.081584   2.847  0.00441 ** 
#> fractureYes      1.411402   1.029705   1.371  0.17047    
#> po2<=60          0.073822   0.857044   0.086  0.93136    
#> ph<7.25          2.354078   1.208804   1.947  0.05148 .  
#> pco>45          -3.018442   1.253448  -2.408  0.01604 *  
#> bic<18          -0.709284   0.909777  -0.780  0.43561    
#> creatin>2        0.295143   1.116925   0.264  0.79159    
#> whiteNon-white   0.565729   0.926828   0.610  0.54160    
#> unconsYes        5.232292   1.226303   4.267 1.98e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 200.16  on 199  degrees of freedom
#> Residual deviance: 120.78  on 180  degrees of freedom
#> AIC: 160.78
#> 
#> Number of Fisher Scoring iterations: 6
#> 

# simpler model (found from a "best" subsets procedure)
icu.mod1 <- glm(died ~ age + sex + cancer + systolic + admit + uncons, 
  data=ICU1, 
  family=binomial)
summary(icu.mod1)
#> 
#> Call:
#> glm(formula = died ~ age + sex + cancer + systolic + admit + 
#>     uncons, family = binomial, data = ICU1)
#> 
#> Coefficients:
#>                 Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)    -5.884702   1.758997  -3.345 0.000821 ***
#> age             0.038875   0.013130   2.961 0.003069 ** 
#> sexMale         0.524194   0.479374   1.093 0.274176    
#> cancerYes       2.386534   0.896958   2.661 0.007798 ** 
#> systolic       -0.011683   0.006833  -1.710 0.087309 .  
#> admitEmergency  3.171332   0.962323   3.295 0.000982 ***
#> unconsYes       3.934575   0.961746   4.091 4.29e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 200.16  on 199  degrees of freedom
#> Residual deviance: 134.38  on 193  degrees of freedom
#> AIC: 148.38
#> 
#> Number of Fisher Scoring iterations: 6
#> 

# even simpler model
icu.mod2 <- glm(died ~ age + cancer  + admit + uncons, 
  data=ICU1, 
  family=binomial)
summary(icu.mod2)
#> 
#> Call:
#> glm(formula = died ~ age + cancer + admit + uncons, family = binomial, 
#>     data = ICU1)
#> 
#> Coefficients:
#>                Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)    -6.86978    1.31882  -5.209 1.90e-07 ***
#> age             0.03718    0.01277   2.911 0.003600 ** 
#> cancerYes       2.09711    0.83847   2.501 0.012381 *  
#> admitEmergency  3.10218    0.91860   3.377 0.000733 ***
#> unconsYes       3.70546    0.87647   4.228 2.36e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 200.16  on 199  degrees of freedom
#> Residual deviance: 139.13  on 195  degrees of freedom
#> AIC: 149.13
#> 
#> Number of Fisher Scoring iterations: 6
#> 

anova(icu.mod2, icu.mod1, icu.full, test="Chisq")
#> Analysis of Deviance Table
#> 
#> Model 1: died ~ age + cancer + admit + uncons
#> Model 2: died ~ age + sex + cancer + systolic + admit + uncons
#> Model 3: died ~ age + sex + service + cancer + renal + infect + cpr + 
#>     systolic + hrtrate + previcu + admit + fracture + po2 + ph + 
#>     pco + bic + creatin + white + uncons
#>   Resid. Df Resid. Dev Df Deviance Pr(>Chi)  
#> 1       195     139.13                       
#> 2       193     134.38  2   4.7582  0.09263 .
#> 3       180     120.78 13  13.5981  0.40274  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

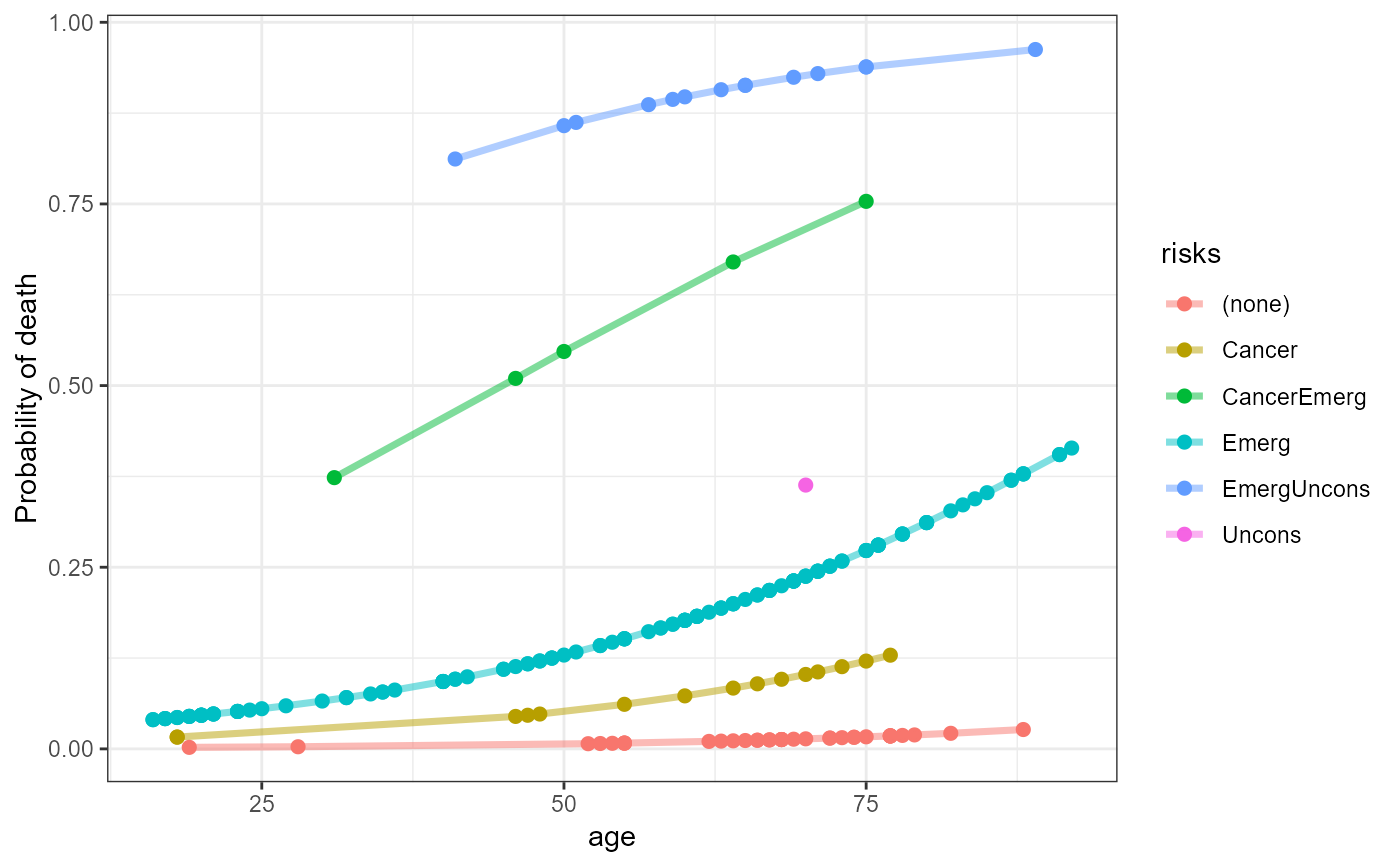
## Reproduce Fig 6.12 from VCD

icu.fit <- data.frame(ICU, prob=predict(icu.mod2, type="response"))

# combine categorical risk factors to a single string
risks <- ICU[, c("cancer", "admit", "uncons")]
risks[,1] <- ifelse(risks[,1]=="Yes", "Cancer", "")
risks[,2] <- ifelse(risks[,2]=="Emergency", "Emerg", "")
risks[,3] <- ifelse(risks[,3]=="Yes", "Uncons", "")
risks <- apply(risks, 1, paste, collapse="")
risks[risks==""] <- "(none)"
icu.fit$risks <- risks

library(ggplot2)
ggplot(icu.fit, aes(x=age, y=prob, color=risks)) +
  geom_point(size=2) +
  geom_line(size=1.25, alpha=0.5) +
  theme_bw() + ylab("Probability of death")