Bertin (1983) used these data to illustrate the cross-classification of data by numerous variables, each of which could have various types and could be assigned to various visual attributes.
Format
A data frame in frequency form (comprising a 5 x 2 x 4 x 2 table) with 80 observations on the following 5 variables.
agean ordered factor with levels
0-9<10-19<20-29<30-49<50+resulta factor with levels
DiedInjuredmodemode of transportation, a factor with levels
4-WheeledBicycleMotorcyclePedestriangendera factor with levels
FemaleMaleFreqa numeric vector
Details
For modeling and visualization purposes, the data can be treated as a 4-way
table using loglinear models and mosaic displays, or as a frequency-weighted
data frame using a binomial response for result ("Died" vs.
"Injured") and plots of predicted probabilities.
age is an ordered factor, but arguably, mode should be treated
as ordered, with levels Pedestrian < Bicycle <
Motorcycle < 4-Wheeled as Bertin does. This affects the
parameterization in models, so we don't do this directly in the data frame.
Examples
# examples
data(Accident)
head(Accident)
#> age result mode gender Freq
#> 1 50+ Died Pedestrian Male 704
#> 2 50+ Died Pedestrian Female 378
#> 3 50+ Died Bicycle Male 396
#> 4 50+ Died Bicycle Female 56
#> 5 50+ Died Motorcycle Male 742
#> 6 50+ Died Motorcycle Female 78
# for graphs, reorder mode
Accident$mode <- ordered(Accident$mode,
levels=levels(Accident$mode)[c(4,2,3,1)])
# Bertin's table
accident_tab <- xtabs(Freq ~ gender + mode + age + result, data=Accident)
structable(mode + gender ~ age + result, data=accident_tab)
#> mode Pedestrian Bicycle Motorcycle 4-Wheeled
#> gender Female Male Female Male Female Male Female Male
#> age result
#> 0-9 Died 89 150 5 26 6 6 65 70
#> Injured 1967 3341 126 378 131 181 1362 1593
#> 10-19 Died 28 70 31 76 54 362 61 150
#> Injured 1495 1827 7218 3407 3587 12311 2593 3543
#> 20-29 Died 24 78 10 55 82 660 107 353
#> Injured 864 1521 609 1565 4010 18558 4361 9084
#> 30-49 Died 49 223 24 146 98 889 199 720
#> Injured 1814 3178 1118 3024 3664 18909 7712 15086
#> 50+ Died 378 704 56 396 78 742 253 513
#> Injured 5449 5206 1030 3863 1387 8597 5552 7423
## Loglinear models
## ----------------
# mutual independence
acc.mod0 <- glm(Freq ~ age + result + mode + gender,
data=Accident,
family=poisson)
LRstats(acc.mod0)
#> Likelihood summary table:
#> AIC BIC LR Chisq Df Pr(>Chisq)
#> acc.mod0 60983 61007 60320 70 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
mosaic(acc.mod0, ~mode + age + gender + result)
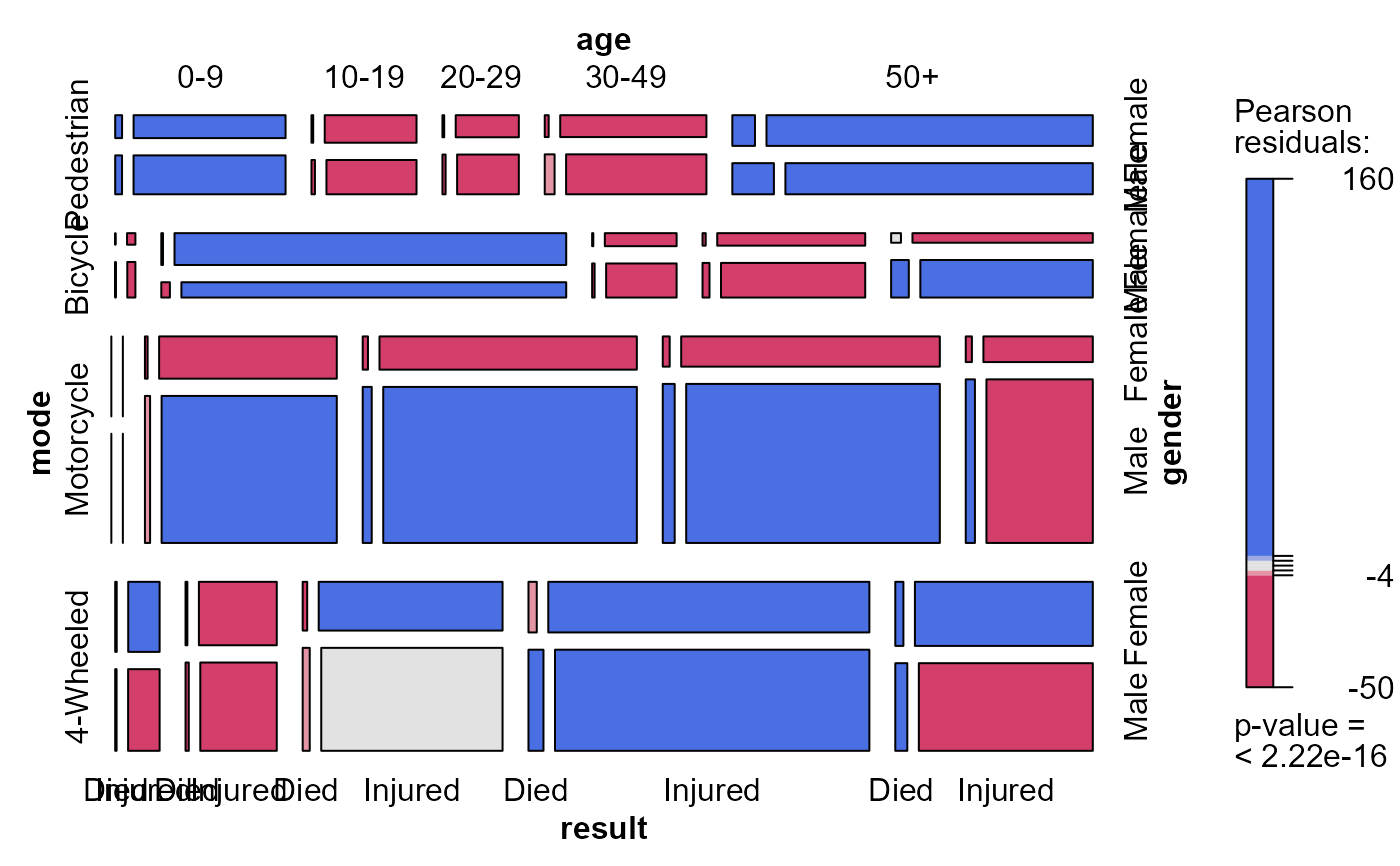 # result as a response
acc.mod1 <- glm(Freq ~ age*mode*gender + result,
data=Accident,
family=poisson)
LRstats(acc.mod1)
#> Likelihood summary table:
#> AIC BIC LR Chisq Df Pr(>Chisq)
#> acc.mod1 2942.4 3040.1 2217.7 39 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
mosaic(acc.mod1, ~mode + age + gender + result,
labeling_args = list(abbreviate = c(gender=1, result=4)))
# result as a response
acc.mod1 <- glm(Freq ~ age*mode*gender + result,
data=Accident,
family=poisson)
LRstats(acc.mod1)
#> Likelihood summary table:
#> AIC BIC LR Chisq Df Pr(>Chisq)
#> acc.mod1 2942.4 3040.1 2217.7 39 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
mosaic(acc.mod1, ~mode + age + gender + result,
labeling_args = list(abbreviate = c(gender=1, result=4)))
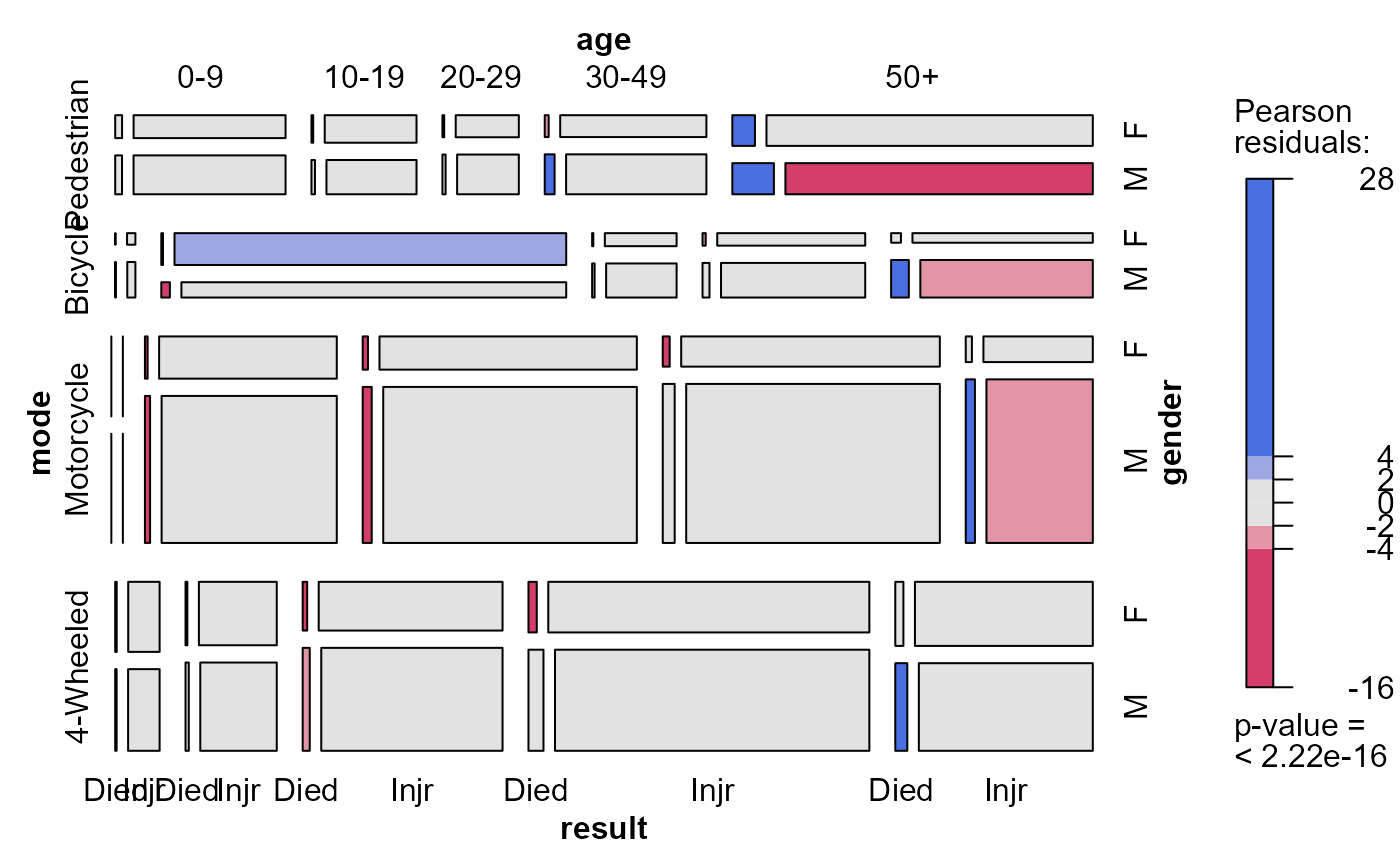 # allow two-way association of result with each explanatory variable
acc.mod2 <- glm(Freq ~ age*mode*gender + result*(age+mode+gender),
data=Accident,
family=poisson)
LRstats(acc.mod2)
#> Likelihood summary table:
#> AIC BIC LR Chisq Df Pr(>Chisq)
#> acc.mod2 968.13 1084.8 227.47 31 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
mosaic(acc.mod2, ~mode + age + gender + result,
labeling_args = list(abbreviate = c(gender=1, result=4)))
# allow two-way association of result with each explanatory variable
acc.mod2 <- glm(Freq ~ age*mode*gender + result*(age+mode+gender),
data=Accident,
family=poisson)
LRstats(acc.mod2)
#> Likelihood summary table:
#> AIC BIC LR Chisq Df Pr(>Chisq)
#> acc.mod2 968.13 1084.8 227.47 31 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
mosaic(acc.mod2, ~mode + age + gender + result,
labeling_args = list(abbreviate = c(gender=1, result=4)))
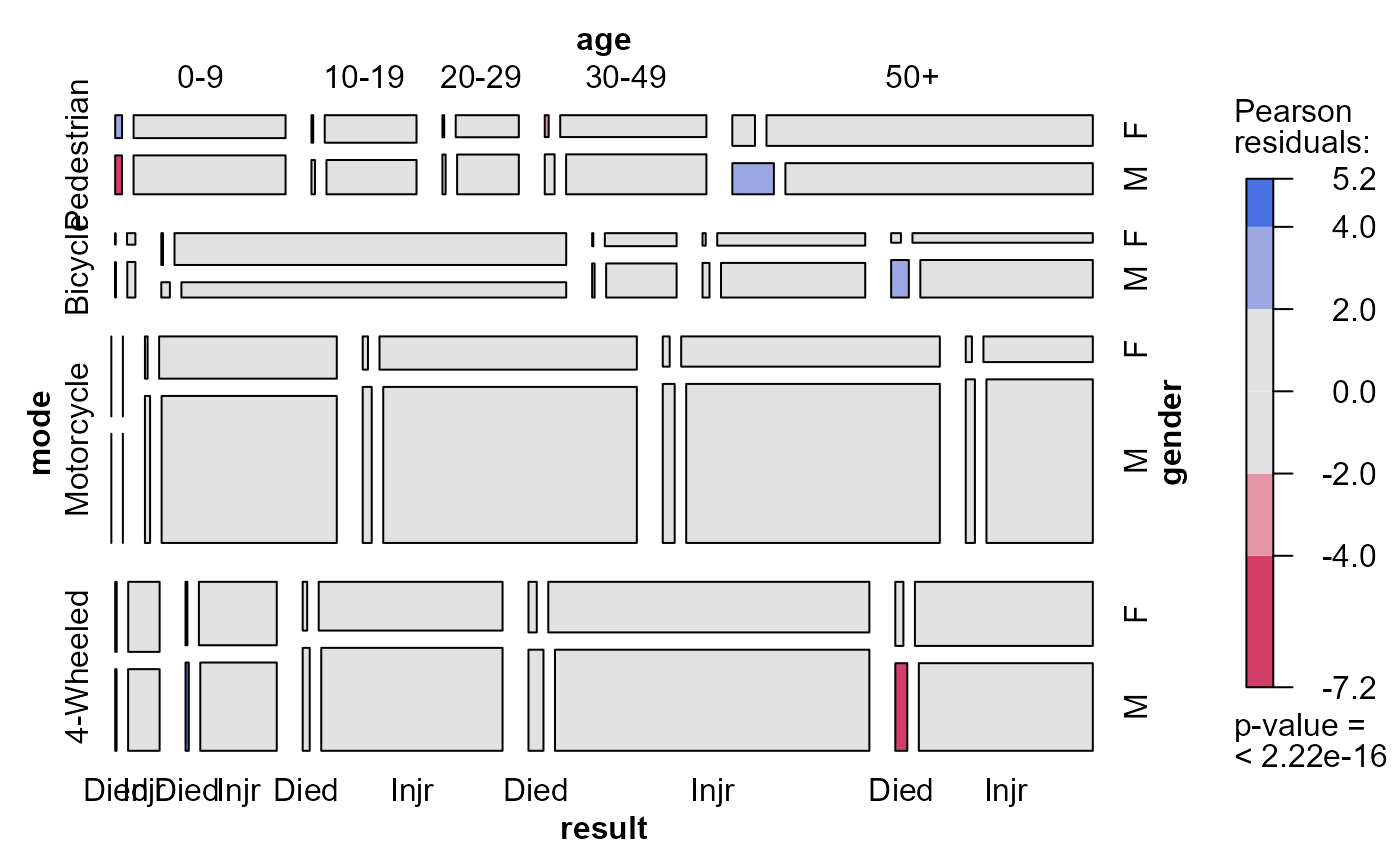 acc.mods <- glmlist(acc.mod0, acc.mod1, acc.mod2)
LRstats(acc.mods)
#> Likelihood summary table:
#> AIC BIC LR Chisq Df Pr(>Chisq)
#> acc.mod0 60983 61007 60320 70 < 2.2e-16 ***
#> acc.mod1 2942 3040 2218 39 < 2.2e-16 ***
#> acc.mod2 968 1085 227 31 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## Binomial (logistic regression) models for result
## ------------------------------------------------
library(car) # for Anova()
#> Loading required package: carData
#>
#> Attaching package: ‘carData’
#> The following object is masked from ‘package:vcdExtra’:
#>
#> Burt
acc.bin1 <- glm(result=='Died' ~ age + mode + gender,
weights=Freq, data=Accident, family=binomial)
Anova(acc.bin1)
#> Analysis of Deviance Table (Type II tests)
#>
#> Response: result == "Died"
#> LR Chisq Df Pr(>Chisq)
#> age 1179.03 4 < 2.2e-16 ***
#> mode 136.82 3 < 2.2e-16 ***
#> gender 467.70 1 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
acc.bin2 <- glm(result=='Died' ~ (age + mode + gender)^2,
weights=Freq, data=Accident, family=binomial)
Anova(acc.bin2)
#> Analysis of Deviance Table (Type II tests)
#>
#> Response: result == "Died"
#> LR Chisq Df Pr(>Chisq)
#> age 1100.82 4 < 2.2e-16 ***
#> mode 136.07 3 < 2.2e-16 ***
#> gender 418.88 1 < 2.2e-16 ***
#> age:mode 122.24 12 < 2.2e-16 ***
#> age:gender 46.86 4 1.631e-09 ***
#> mode:gender 21.94 3 6.702e-05 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
acc.bin3 <- glm(result=='Died' ~ (age + mode + gender)^3,
weights=Freq, data=Accident, family=binomial)
Anova(acc.bin3)
#> Analysis of Deviance Table (Type II tests)
#>
#> Response: result == "Died"
#> LR Chisq Df Pr(>Chisq)
#> age 1100.82 4 < 2.2e-16 ***
#> mode 136.07 3 < 2.2e-16 ***
#> gender 418.88 1 < 2.2e-16 ***
#> age:mode 122.24 12 < 2.2e-16 ***
#> age:gender 46.86 4 1.631e-09 ***
#> mode:gender 21.94 3 6.702e-05 ***
#> age:mode:gender 13.02 12 0.3675
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# compare models
anova(acc.bin1, acc.bin2, acc.bin3, test="Chisq")
#> Analysis of Deviance Table
#>
#> Model 1: result == "Died" ~ age + mode + gender
#> Model 2: result == "Died" ~ (age + mode + gender)^2
#> Model 3: result == "Died" ~ (age + mode + gender)^3
#> Resid. Df Resid. Dev Df Deviance Pr(>Chi)
#> 1 71 64599
#> 2 52 64384 19 214.445 <2e-16 ***
#> 3 40 64371 12 13.022 0.3675
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# visualize probability of death with effect plots
if (FALSE) { # \dontrun{
library(effects)
plot(allEffects(acc.bin1), ylab='Pr (Died)')
plot(allEffects(acc.bin2), ylab='Pr (Died)')
} # }
#
acc.mods <- glmlist(acc.mod0, acc.mod1, acc.mod2)
LRstats(acc.mods)
#> Likelihood summary table:
#> AIC BIC LR Chisq Df Pr(>Chisq)
#> acc.mod0 60983 61007 60320 70 < 2.2e-16 ***
#> acc.mod1 2942 3040 2218 39 < 2.2e-16 ***
#> acc.mod2 968 1085 227 31 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## Binomial (logistic regression) models for result
## ------------------------------------------------
library(car) # for Anova()
#> Loading required package: carData
#>
#> Attaching package: ‘carData’
#> The following object is masked from ‘package:vcdExtra’:
#>
#> Burt
acc.bin1 <- glm(result=='Died' ~ age + mode + gender,
weights=Freq, data=Accident, family=binomial)
Anova(acc.bin1)
#> Analysis of Deviance Table (Type II tests)
#>
#> Response: result == "Died"
#> LR Chisq Df Pr(>Chisq)
#> age 1179.03 4 < 2.2e-16 ***
#> mode 136.82 3 < 2.2e-16 ***
#> gender 467.70 1 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
acc.bin2 <- glm(result=='Died' ~ (age + mode + gender)^2,
weights=Freq, data=Accident, family=binomial)
Anova(acc.bin2)
#> Analysis of Deviance Table (Type II tests)
#>
#> Response: result == "Died"
#> LR Chisq Df Pr(>Chisq)
#> age 1100.82 4 < 2.2e-16 ***
#> mode 136.07 3 < 2.2e-16 ***
#> gender 418.88 1 < 2.2e-16 ***
#> age:mode 122.24 12 < 2.2e-16 ***
#> age:gender 46.86 4 1.631e-09 ***
#> mode:gender 21.94 3 6.702e-05 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
acc.bin3 <- glm(result=='Died' ~ (age + mode + gender)^3,
weights=Freq, data=Accident, family=binomial)
Anova(acc.bin3)
#> Analysis of Deviance Table (Type II tests)
#>
#> Response: result == "Died"
#> LR Chisq Df Pr(>Chisq)
#> age 1100.82 4 < 2.2e-16 ***
#> mode 136.07 3 < 2.2e-16 ***
#> gender 418.88 1 < 2.2e-16 ***
#> age:mode 122.24 12 < 2.2e-16 ***
#> age:gender 46.86 4 1.631e-09 ***
#> mode:gender 21.94 3 6.702e-05 ***
#> age:mode:gender 13.02 12 0.3675
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# compare models
anova(acc.bin1, acc.bin2, acc.bin3, test="Chisq")
#> Analysis of Deviance Table
#>
#> Model 1: result == "Died" ~ age + mode + gender
#> Model 2: result == "Died" ~ (age + mode + gender)^2
#> Model 3: result == "Died" ~ (age + mode + gender)^3
#> Resid. Df Resid. Dev Df Deviance Pr(>Chi)
#> 1 71 64599
#> 2 52 64384 19 214.445 <2e-16 ***
#> 3 40 64371 12 13.022 0.3675
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# visualize probability of death with effect plots
if (FALSE) { # \dontrun{
library(effects)
plot(allEffects(acc.bin1), ylab='Pr (Died)')
plot(allEffects(acc.bin2), ylab='Pr (Died)')
} # }
#
