A tiny hypothetical dataset to illustrate one-way MANOVA.
A dogfood manufacturer wanted to study preference for different dogfood formulas, two of their own
("Old", "New") and two from other manufacturers ("Major", "Alps"). In a between-dog design, 4 dogs
were presented with a bowl of one formula and the time to start eating and amount eaten were recorded.
Usage
data("dogfood")Format
A data frame with 16 observations on the following 3 variables.
formulafactor, a factor with levels
Old,New,Major,Alpsstartnumeric, time to start eating
amountnumeric, amount eaten
Source
Used in my Psych 6140 lecture notes, http://friendly.apps01.yorku.ca/psy6140/
Details
In addition to testing the overall effects of formula,
three useful (and orthogonal) contrasts can specified for this 3-df factor:
Oursvs.Theirs, with weightsc(1, 1, -1, -1)Majorvs.Alps, with weightsc(0, 0, 1, -1)Oldvs.New, with weightsc(1, -1, 0, 0)
Because these are orthogonal contrasts, they fully decompose the main effect of formula,
in that their sum of squares add to the overall sum of squares.
Examples
data(dogfood)
library(car)
library(candisc)
#>
#> Attaching package: 'candisc'
#> The following object is masked from 'package:stats':
#>
#> cancor
# make some boxplots
op <- par(mfrow = c(1,2))
boxplot(start ~ formula, data = dogfood)
points(start ~ formula, data = dogfood, pch=16, cex = 1.2)
boxplot(amount ~ formula, data = dogfood)
points(amount ~ formula, data = dogfood, pch=16, cex = 1.2)
 par(op)
# setup contrasts to test interesting comparisons
C <- matrix(
c( 1, 1, -1, -1, #Ours vs. Theirs
0, 0, 1, -1, #Major vs. Alps
1, -1, 0, 0), #New vs. Old
nrow=4, ncol=3)
# assign these to the formula factor
contrasts(dogfood$formula) <- C
# re-fit the model
dogfood.mod <- lm(cbind(start, amount) ~ formula, data=dogfood)
dogfood.mod <- lm(cbind(start, amount) ~ formula, data=dogfood)
Anova(dogfood.mod)
#>
#> Type II MANOVA Tests: Pillai test statistic
#> Df test stat approx F num Df den Df Pr(>F)
#> formula 3 0.70178 2.1623 6 24 0.08289 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
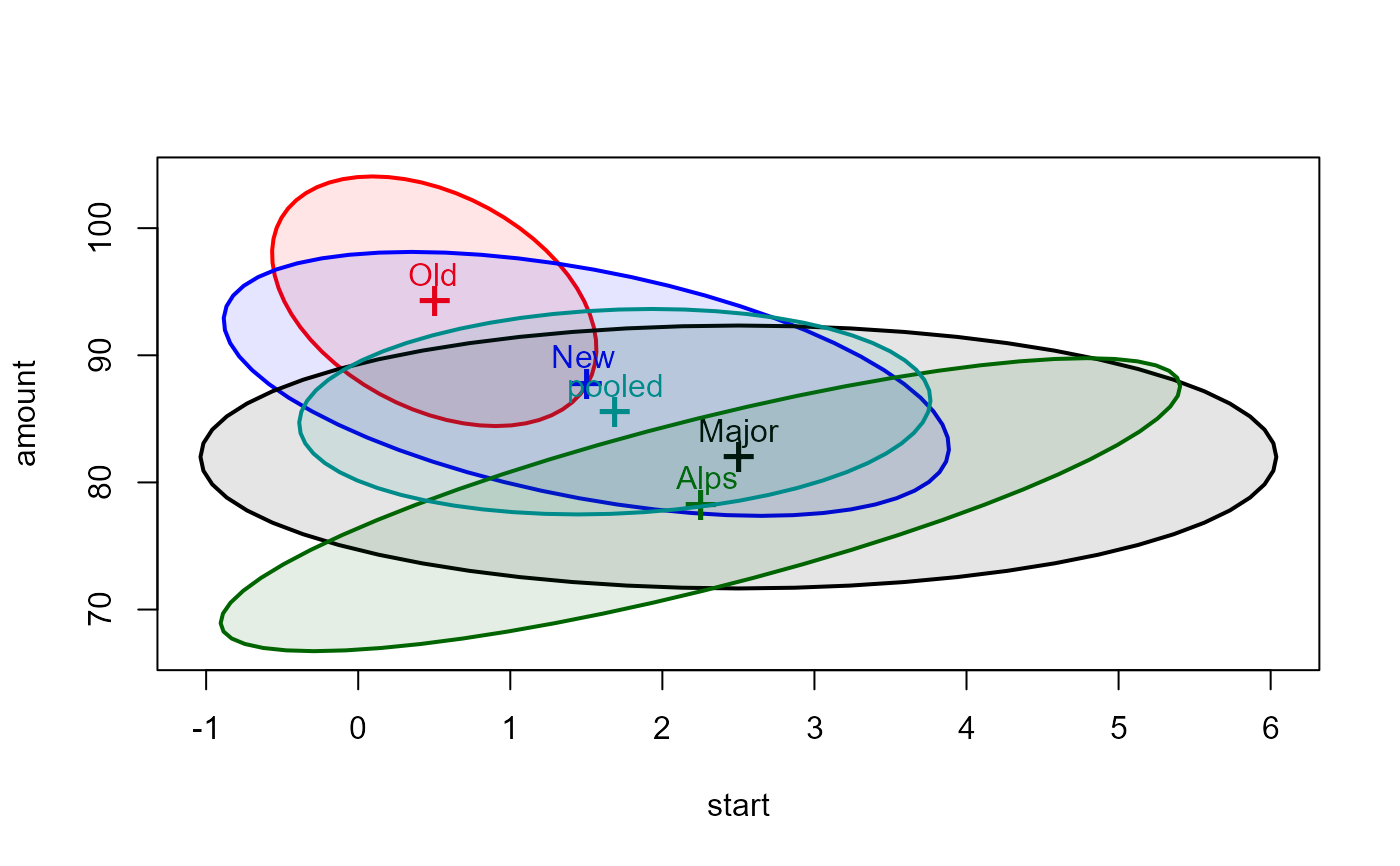
# data ellipses
covEllipses(cbind(start, amount) ~ formula, data=dogfood,
fill = TRUE, fill.alpha = 0.1)
par(op)
# setup contrasts to test interesting comparisons
C <- matrix(
c( 1, 1, -1, -1, #Ours vs. Theirs
0, 0, 1, -1, #Major vs. Alps
1, -1, 0, 0), #New vs. Old
nrow=4, ncol=3)
# assign these to the formula factor
contrasts(dogfood$formula) <- C
# re-fit the model
dogfood.mod <- lm(cbind(start, amount) ~ formula, data=dogfood)
dogfood.mod <- lm(cbind(start, amount) ~ formula, data=dogfood)
Anova(dogfood.mod)
#>
#> Type II MANOVA Tests: Pillai test statistic
#> Df test stat approx F num Df den Df Pr(>F)
#> formula 3 0.70178 2.1623 6 24 0.08289 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# data ellipses
covEllipses(cbind(start, amount) ~ formula, data=dogfood,
fill = TRUE, fill.alpha = 0.1)
 # test these contrasts with multivariate tests
linearHypothesis(dogfood.mod, "formula1", title="Ours vs. Theirs")
#>
#> Sum of squares and products for the hypothesis:
#> start amount
#> start 7.5625 -59.8125
#> amount -59.8125 473.0625
#>
#> Sum of squares and products for error:
#> start amount
#> start 25.75 11.75
#> amount 11.75 390.25
#>
#> Multivariate Tests: Ours vs. Theirs
#> Df test stat approx F num Df den Df Pr(>F)
#> Pillai 1 0.6252849 9.177818 2 11 0.0045223 **
#> Wilks 1 0.3747151 9.177818 2 11 0.0045223 **
#> Hotelling-Lawley 1 1.6686941 9.177818 2 11 0.0045223 **
#> Roy 1 1.6686941 9.177818 2 11 0.0045223 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
linearHypothesis(dogfood.mod, "formula2", title="Old vs. New")
#>
#> Sum of squares and products for the hypothesis:
#> start amount
#> start 0.125 1.875
#> amount 1.875 28.125
#>
#> Sum of squares and products for error:
#> start amount
#> start 25.75 11.75
#> amount 11.75 390.25
#>
#> Multivariate Tests: Old vs. New
#> Df test stat approx F num Df den Df Pr(>F)
#> Pillai 1 0.0685104 0.4045209 2 11 0.67683
#> Wilks 1 0.9314896 0.4045209 2 11 0.67683
#> Hotelling-Lawley 1 0.0735493 0.4045209 2 11 0.67683
#> Roy 1 0.0735493 0.4045209 2 11 0.67683
linearHypothesis(dogfood.mod, "formula3", title="Alps vs. Major")
#>
#> Sum of squares and products for the hypothesis:
#> start amount
#> start 2 -13.0
#> amount -13 84.5
#>
#> Sum of squares and products for error:
#> start amount
#> start 25.75 11.75
#> amount 11.75 390.25
#>
#> Multivariate Tests: Alps vs. Major
#> Df test stat approx F num Df den Df Pr(>F)
#> Pillai 1 0.2476229 1.810164 2 11 0.20912
#> Wilks 1 0.7523771 1.810164 2 11 0.20912
#> Hotelling-Lawley 1 0.3291208 1.810164 2 11 0.20912
#> Roy 1 0.3291208 1.810164 2 11 0.20912
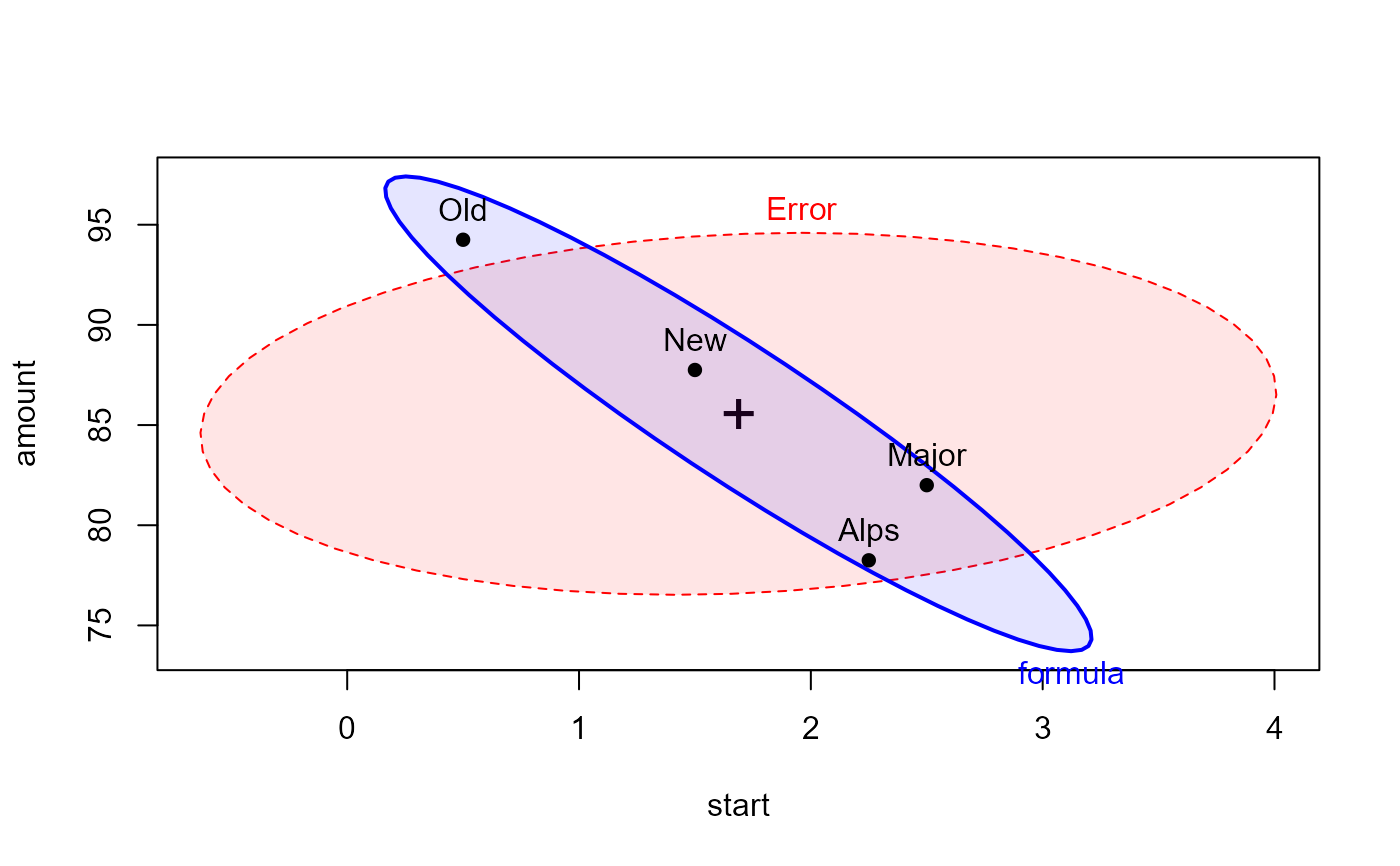
heplot(dogfood.mod, fill = TRUE, fill.alpha = 0.1)
# test these contrasts with multivariate tests
linearHypothesis(dogfood.mod, "formula1", title="Ours vs. Theirs")
#>
#> Sum of squares and products for the hypothesis:
#> start amount
#> start 7.5625 -59.8125
#> amount -59.8125 473.0625
#>
#> Sum of squares and products for error:
#> start amount
#> start 25.75 11.75
#> amount 11.75 390.25
#>
#> Multivariate Tests: Ours vs. Theirs
#> Df test stat approx F num Df den Df Pr(>F)
#> Pillai 1 0.6252849 9.177818 2 11 0.0045223 **
#> Wilks 1 0.3747151 9.177818 2 11 0.0045223 **
#> Hotelling-Lawley 1 1.6686941 9.177818 2 11 0.0045223 **
#> Roy 1 1.6686941 9.177818 2 11 0.0045223 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
linearHypothesis(dogfood.mod, "formula2", title="Old vs. New")
#>
#> Sum of squares and products for the hypothesis:
#> start amount
#> start 0.125 1.875
#> amount 1.875 28.125
#>
#> Sum of squares and products for error:
#> start amount
#> start 25.75 11.75
#> amount 11.75 390.25
#>
#> Multivariate Tests: Old vs. New
#> Df test stat approx F num Df den Df Pr(>F)
#> Pillai 1 0.0685104 0.4045209 2 11 0.67683
#> Wilks 1 0.9314896 0.4045209 2 11 0.67683
#> Hotelling-Lawley 1 0.0735493 0.4045209 2 11 0.67683
#> Roy 1 0.0735493 0.4045209 2 11 0.67683
linearHypothesis(dogfood.mod, "formula3", title="Alps vs. Major")
#>
#> Sum of squares and products for the hypothesis:
#> start amount
#> start 2 -13.0
#> amount -13 84.5
#>
#> Sum of squares and products for error:
#> start amount
#> start 25.75 11.75
#> amount 11.75 390.25
#>
#> Multivariate Tests: Alps vs. Major
#> Df test stat approx F num Df den Df Pr(>F)
#> Pillai 1 0.2476229 1.810164 2 11 0.20912
#> Wilks 1 0.7523771 1.810164 2 11 0.20912
#> Hotelling-Lawley 1 0.3291208 1.810164 2 11 0.20912
#> Roy 1 0.3291208 1.810164 2 11 0.20912
heplot(dogfood.mod, fill = TRUE, fill.alpha = 0.1)
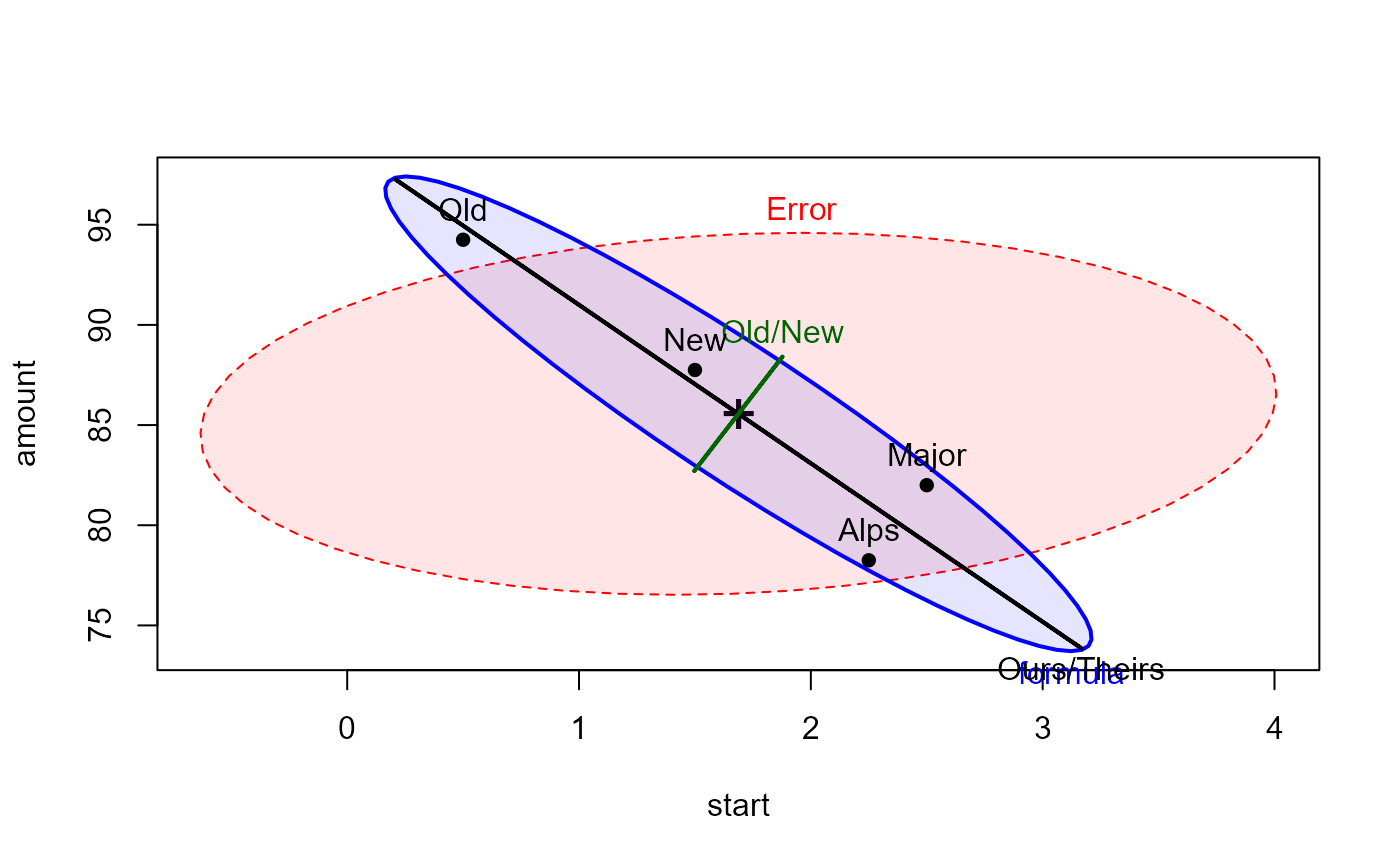 # display contrasts in the heplot
hyp <- list("Ours/Theirs" = "formula1",
"Old/New" = "formula2")
heplot(dogfood.mod, hypotheses = hyp,
fill = TRUE, fill.alpha = 0.1)
# display contrasts in the heplot
hyp <- list("Ours/Theirs" = "formula1",
"Old/New" = "formula2")
heplot(dogfood.mod, hypotheses = hyp,
fill = TRUE, fill.alpha = 0.1)
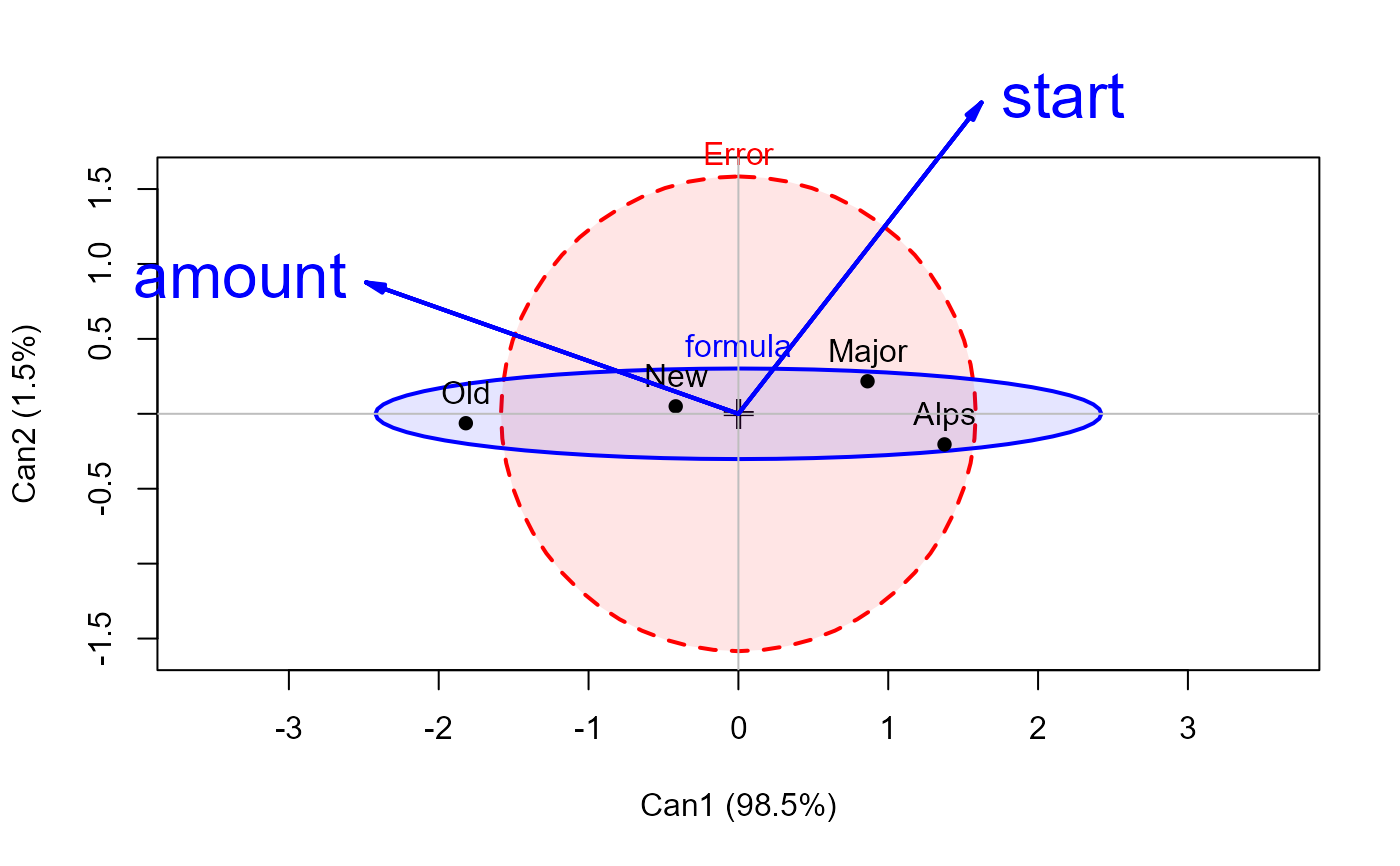 dogfood.can <- candisc(dogfood.mod, data=dogfood)
heplot(dogfood.can,
fill = TRUE, fill.alpha = 0.1,
lwd = 2, var.lwd = 2, var.cex = 2)
dogfood.can <- candisc(dogfood.mod, data=dogfood)
heplot(dogfood.can,
fill = TRUE, fill.alpha = 0.1,
lwd = 2, var.lwd = 2, var.cex = 2)
 #> Vector scale factor set to 2.635145
#> Vector scale factor set to 2.635145