Robust Multivariate Linear Models

Michael Friendly

2026-08-23

Abstract

This vignette describes the theory behind, and demonstrates the use of, the robmlm() function from the heplots package, which provides robust estimation for multivariate linear models (MLMs) using iteratively reweighted least squares (IRLS).

It illustrates the central ideas behind robust estimation for MLMs, how the IRLS algorithm works, and presents examples of plots that help understand how robust models can contribute to data analysis. It uses two examples, one for a MANOVA design and another for a multivariate multiple regression to show features of robust methods and the graphical methods of this package that help to understand them.

Load packages

I use the following packages here:

library(heplots)
library(candisc)
library(ggplot2)
library(dplyr)
library(mvinfluence)

Introduction

Multivariate linear models (MLMs) extend the familiar univariate linear regression framework to situations where multiple response variables are modeled simultaneously as linear functions of a common set of predictor variables. While classical multivariate least squares estimation provides optimal results under ideal conditions (multivariate normality and absence of outliers), real-world data often violate these assumptions. The presence of outliers, heavy-tailed distributions, or other departures from normality can severely compromise the reliability of classical estimators, leading to biased parameter estimates and inflated error rates in hypothesis testing.

The need for robust estimation in multivariate regression has been recognized since the early development of robust statistical methods (Huber, 1964; Tukey, 1960). Outliers in multivariate data can be particularly problematic because they may not be readily apparent when examining univariate marginal distributions, yet can exert substantial leverage on the fitted model. Furthermore, the curse of dimensionality means that as the number of response variables increases, the probability of encountering at least one outlying observation grows rapidly.

Robust multivariate regression methods aim to provide reliable parameter estimates and inference procedures that remain stable in the presence of outlying observations. As noted by Rousseeuw, Van Aelst, Van Driessen, & Gulló (2004),

“The main advantage of robust regression is that it provides reliable results even when some of the assumptions of classical regression are violated.”

Several approaches have been developed for robust multivariate regression, including M-estimators, S-estimators (Rousseeuw & Yohai, 1984), and MM-estimators (Yohai, 1987). Each approach offers different trade-offs between robustness properties, computational efficiency, and statistical efficiency under ideal conditions. See the CRAN Task View: Robust Statistical Methods for an extensive list of robust methods in R. The vignette for the rrcov package, obtained by vignette(package = "rrcov"), contains a general overview of multivariate robust methods.

The method implemented in the robmlm() function belongs to the class of M-estimators, which generalize maximum likelihood estimation by replacing the likelihood function with a more robust objective function.

The key idea is to relax the least squares criterion of minimizing $Q(\mathbf{e}) = \Sigma e_i^2 = \Sigma (y_i - \hat{y}_i)^2$ by considering more general functions $Q(\mathbf{e}, \rho)$, where the function $\rho (e_i)$ can be chosen to reduce the impact of large outliers. In these terms,

• OLS uses $\rho(e_i) = e_i^2$
• $L_1$ estimation uses $\rho(e_i) = \vert e_i \vert$, the least absolute values
• A bit more complicated, the biweight function uses a squared measure of error up to some value $c$ and then levels off thereafter,

$$\rho(e_i) = \begin{cases} \left[ 1 - \left( \frac{e_i}{c} \right)^2 \right]^2 & |e_i| \leq c, \\ 1 & |e_i| > c. \end{cases}$$

These functions look like this in a graph. The biweight function has a property like Windsorizing— the squared error remains constant for residuals $e_i > c$, with $c = 4.685$ for MASS::psi.bisquare().

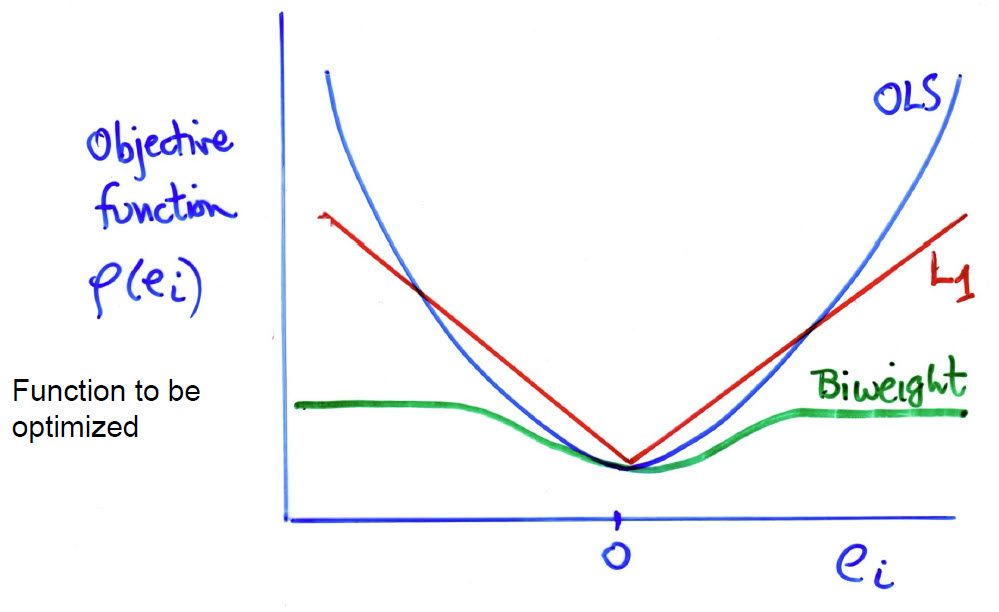
Figure 1: Diagram ploting the function $\rho(e_i)$ of the contributions of the residuals $e_i$ to what is minimized in various fitting methods.

Methodology: Iteratively Reweighted Least Squares (IRLS)

The robmlm() function implements robust multivariate linear model fitting using Iteratively Reweighted Least Squares (IRLS), a flexible and computationally efficient approach that belongs to the family of M-estimators. The core idea behind IRLS is to iteratively downweight observations that appear to be outliers based on their residual distances from the fitted model.

The IRLS Algorithm

The IRLS algorithm for robust multivariate regression is shown in the figure below.

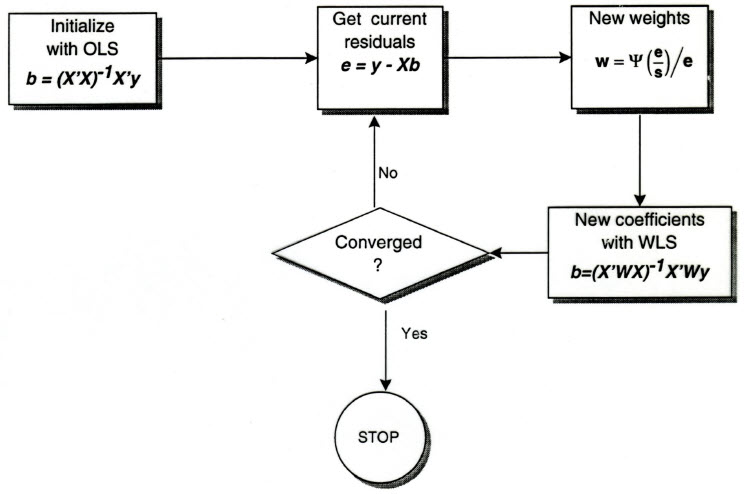
Figure 2: Flowchart for the iteratively reweighted least squares algorithm

The method proceeds as follows:

1. Initialization: Begin with an initial estimate of the regression coefficients, typically obtained from ordinary least squares (OLS).

2. Residual calculation: Compute the multivariate residuals for each observation: $$\mathbf{r}_i = \mathbf{y}_i - \mathbf{X}_i\hat{\boldsymbol{\beta}}$$ where $\mathbf{y}_i$ is the $p \times 1$ response vector for observation $i$, $\mathbf{X}_i$ is the corresponding row of the design matrix, and $\hat{\boldsymbol{\beta}}$ is the current estimate of the coefficient matrix.

3. Distance computation: Calculate the squared Mahalanobis distance of each residual vector from the origin: $$d_i^2 = \mathbf{r}_i^T \mathbf{S}^{-1} \mathbf{r}_i$$ where $\mathbf{S}$ is a robust estimate of the residual covariance matrix, computed using MASS::cov.trob().

4. Weight assignment: Assign weights to each observation based on their residual distances. Observations with larger distances receive smaller weights, effectively downweighting potential outliers: $$w_i = \rho(d_i^2)$$ where $\rho(\cdot)$ is a weight function that decreases as the distance increases.

5. Weighted Least Squares: Update the coefficient estimates using weighted least squares: $$\hat{\boldsymbol{\beta}}^{(new)} = (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}\mathbf{Y}$$ where $\mathbf{W}$ is a diagonal matrix of weights.

6. Convergence check: Repeat steps 2-5 until convergence, typically assessed by monitoring changes in the coefficient estimates or weights between iterations.

Features of the Implementation

The robmlm() implementation incorporates several important features:

• Robust covariance estimation: The use of MASS::cov.trob() provides a robust estimate of the residual covariance matrix, which is crucial for computing meaningful Mahalanobis distances in the presence of outliers. This uses the multivariate $t$ distribution that allows for longer tails. (There are other robust covariance estimators, such as Minimum Covariance Determinant (MCD) and Minimum Volume Ellipse (MVE), which have a high tolerance—breakdown-bound– for outliers. These might come to a future version of robmlm().)

• Inheritance Structure: The returned object inherits from both "mlm" and "lm" classes, ensuring compatibility with existing R infrastructure for linear models while adding robust-specific methods.

• Weight Preservation: The final weights are preserved in the fitted object, allowing users to identify influential observations and assess the impact of the robust fitting procedure.

• Diagnostic Capabilities: The plot.robmlm() method provides immediate visual feedback on the weighting scheme, plotting final weights against case numbers to highlight observations that were down-weighted during the fitting process.

• Visualization methods: Because a fitted robmlm object inherits the "mlm" class, it works directly with heplots’ existing diagnostic and hypothesis-test plots. distancePlot() plots the Mahalanobis distances of the model-matrix predictors against the distances of the residuals, so cases with both high leverage and a large residual — and so likely down-weighted during IRLS — stand out just as they would for a classical mlm. heplot() goes further: fitting the classical and robust models separately and overlaying the robust H and E ellipses on the classical model’s plot (add = TRUE) gives a direct geometric view of how down-weighting outliers reshapes the hypothesis and error variation — typically a visibly smaller E ellipse for the robust fit. See the example below.

Theoretical Properties

The IRLS approach offers several desirable theoretical properties:

• Breakdown Point: While not achieving the highest possible breakdown point, M-estimators like those implemented in IRLS can handle a reasonable proportion of outliers before completely breaking down.

• Influence Function: The bounded influence function of M-estimators ensures that no single observation can have unlimited impact on the final estimates.

• Asymptotic Efficiency: Under ideal conditions (no outliers, multivariate normality), robust M-estimators achieve high efficiency relative to classical least squares estimators.

• Equivariance: The robust estimates maintain appropriate equivariance properties under linear transformations of the data.

Example: Pottery Data

We begin with a simple but illustrative example using the pottery composition data from the carData package. This dataset contains measurements of five chemical elements (Al, Fe, Mg, Ca, Na) in pottery samples from four different archaeological sites. The goal is to determine whether the chemical composition differs significantly across sites, a classic one-way MANOVA problem. Alternatively, it can be framed as a problem in discriminant analysis, asking whether these chemical elements can be used to distinguish among the sites.

library(heplots)
library(carData)
library(car)

# Load the pottery data
data(Pottery, package = "carData")
head(Pottery)
#>        Site   Al   Fe   Mg   Ca   Na
#> 1 Llanedyrn 14.4 7.00 4.30 0.15 0.51
#> 2 Llanedyrn 13.8 7.08 3.43 0.12 0.17
#> 3 Llanedyrn 14.6 7.09 3.88 0.13 0.20
#> 4 Llanedyrn 11.5 6.37 5.64 0.16 0.14
#> 5 Llanedyrn 13.8 7.06 5.34 0.20 0.20
#> 6 Llanedyrn 10.9 6.26 3.47 0.17 0.22

The pottery dataset contains 26 observations with measurements of five response variables representing chemical concentrations. Let’s examine the basic structure:

str(Pottery)
#> 'data.frame':    26 obs. of  6 variables:
#>  $ Site: Factor w/ 4 levels "AshleyRails",..: 4 4 4 4 4 4 4 4 4 4 ...
#>  $ Al  : num  14.4 13.8 14.6 11.5 13.8 10.9 10.1 11.6 11.1 13.4 ...
#>  $ Fe  : num  7 7.08 7.09 6.37 7.06 6.26 4.26 5.78 5.49 6.92 ...
#>  $ Mg  : num  4.3 3.43 3.88 5.64 5.34 3.47 4.26 5.91 4.52 7.23 ...
#>  $ Ca  : num  0.15 0.12 0.13 0.16 0.2 0.17 0.2 0.18 0.29 0.28 ...
#>  $ Na  : num  0.51 0.17 0.2 0.14 0.2 0.22 0.18 0.16 0.3 0.2 ...

The pottery samples are not evenly distributed across the sites. The most come from Llanedryn; there are only two from Caldicot.

table(Pottery$Site)
#> 
#> AshleyRails    Caldicot  IsleThorns   Llanedyrn 
#>           5           2           5          14

Classical MANOVA

We begin with the standard MANOVA model, and then examine some diagnostic plots.

# Classical MANOVA model
pottery.mlm <- lm(cbind(Al, Fe, Mg, Ca, Na) ~ Site, data = Pottery)
Anova(pottery.mlm)
#> 
#> Type II MANOVA Tests: Pillai test statistic
#>      Df test stat approx F num Df den Df  Pr(>F)    
#> Site  3      1.55      4.3     15     60 2.4e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Chisquare QQ plot: As an initial check, a cqplot() of the model gives a $\chi^2$ QQ plot of the residuals from the model, which would identify badly fit observations. None seem particularly large here.

cqplot(pottery.mlm, id.n = 5)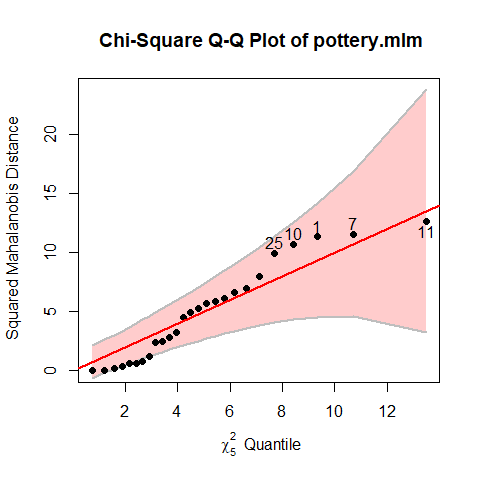

Figure 3: Chisquare QQ plot for the Pottery model.

Influence plot: An influence plot for this model, done using mvinfluence::influencePlot() plots the leverage multivariate hat-values for the predictors (site) against squared multivariate studentized residuals, using the size of the point symbol proportional to a multivariate generalization of Cook’s D statistic.

res <- influencePlot(pottery.mlm, id.n = 2)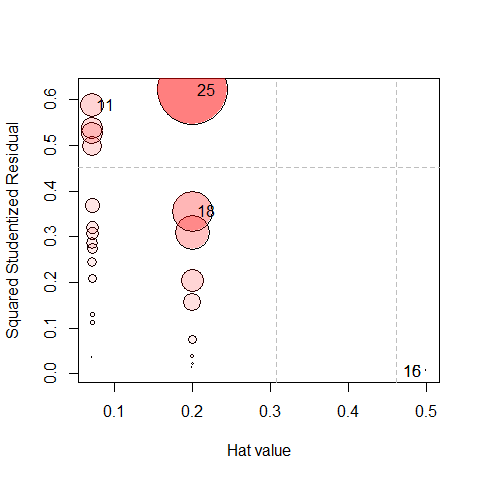

Figure 4: Influence plot for the Pottery model.

res |>
  arrange(desc(CookD))
#>          H        Q   CookD       L       R
#> 25 0.20000 0.621766 0.68394 0.25000 0.77721
#> 18 0.20000 0.355067 0.39057 0.25000 0.44383
#> 11 0.07143 0.587152 0.23067 0.07692 0.63232
#> 16 0.50000 0.006379 0.01754 1.00000 0.01276
#> 15 0.50000 0.006379 0.01754 1.00000 0.01276

Because site is a factor, the hat-values are inversely proportional to the sample size. Points for Llanedryn ($n=14$) are in the left-most column, followed by AshleyRails and IsleThorns (each with $n=5$) and then Caldicot ($n=14$).

Here, case 25 stands out with the largest value of Cook’s D, followed by 18 and 11.

Robust MANOVA

Now, fit the robust model using robmlm(). Because this uses an iterative IRLS method, points that might not seem unusual in the initial model can become more noteworthy when the extreme observations are down-weighted in a subsequent iteration.

# Robust MANOVA model
pottery.rlm <- robmlm(cbind(Al, Fe, Mg, Ca, Na) ~ Site, data = Pottery)
Anova(pottery.rlm)
#> 
#> Type II MANOVA Tests: Pillai test statistic
#>      Df test stat approx F num Df den Df  Pr(>F)    
#> Site  3      1.98     6.55     15     51 1.7e-07 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Let’s compare the results. From the results of Anova() above, you can see that the $F$ statistic for the robust model is greater than that for OLS, which suggests that possible outliers may have reduced the strength of evidence for differences among the sites.

It is useful to compare the coefficients of the two models, and for this, their relative difference is a useful metric. The simple function reldiff() expresses these as the signed percent of difference between the classical and robust estimates.

b.mlm <- coef(pottery.mlm)
b.rlm <- coef(pottery.rlm)

reldiff <- function(x, y, pct=TRUE) {
  res <- abs(x - y) / x
  if (pct) res <- 100 * res
  res
}

reldiff(b.mlm, b.rlm)
#>                     Al      Fe      Mg      Ca      Na
#> (Intercept)      3.616  20.480  2.5908  10.333  0.6925
#> SiteCaldicot   -11.145   7.934  0.4832   2.211 16.6192
#> SiteIsleThorns  64.510 136.881 25.1469 -21.792  1.9605
#> SiteLlanedyrn  -11.559   9.969  2.0078   6.241 22.7443

Among these, the coefficients for IsleThorns are quite different for most of the variables.

Examining the Robust Weights

The robust fitting procedure assigns weights to each observation based on their deviation from the fitted model. Observations that appear to be outliers receive lower weights. The plot() method for a "roblm" object gives an index plot of the weight values.

# Plot the weights from robust fitting
plot(pottery.rlm, col=Pottery$Site, segments=TRUE)
xloc <- c(7.5, 15.5, 19.5, 24)
text(xloc, rep(c(1.0, 1.05), length=5), 
     levels(Pottery$Site), pos =3, xpd = TRUE)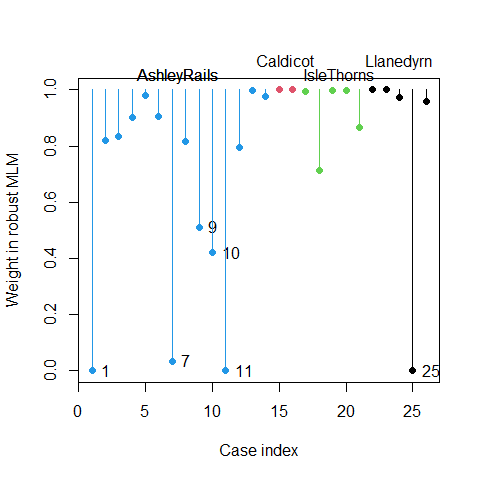

Figure 5: Weights from robust MANOVA fitting showing potential outliers

The weight plot reveals which observations were considered potentially problematic during the robust fitting process. Observations with weights substantially below 1.0 were down-weighted, indicating they may be outliers in the multivariate space defined by the five chemical measurements.

Distance Plot

distancePlot() gives a complementary view of the same idea. It plots the Mahalanobis distances of the Site predictors (the model matrix X) against the distances of the residuals from the robust fit, labeling cases beyond the cutoff lines (dashed, level = 0.975 by default). This plot method, due to Rousseeuw & van Zomeren (1990, 1991) and Rousseeuw et al. (2004), helps you see WHY observations are downweighted, by combining information on regression outliers (unusual in the Y responses) and leverage points (unusual in the Xs).

distancePlot(pottery.rlm)
#> 0.975 X, Y distance cutoffs: 3.058 3.582

Figure 6: Distance plot for the robust Pottery model: Mahalanobis distances of the Site predictors vs. distances of the residuals.

Case 25 – already flagged with the largest Cook’s D in the classical influence plot above – again stands out, here with an unusually large residual distance. Cases 15 and 16 stand out instead on the predictor (Site) side, reflecting their group’s small sample size rather than an unusual response pattern.

Hypothesis-Error (HE) plots

HE plots provide a visual representation of the multivariate hypothesis test by showing the relationship between hypothesis and error variation in a reduced dimensional space. We’ll create HE plots for the first two variables (Al and Fe) and compare the classical and robust fits.

# Classical HE plot for Al and Fe
heplot(pottery.mlm, variables = c("Al", "Fe"), 
       main = "Classical vs Robust MANOVA: Al vs Fe",
       col = c("blue", "blue"), fill = TRUE, fill.alpha = 0.2)

# Overlay robust HE plot
heplot(pottery.rlm, variables = c("Al", "Fe"), 
       add = TRUE, error.ellipse = TRUE,
       col = c("red", "red"), 
       fill = TRUE, fill.alpha = 0.2, lty = 2)

# Add legend
legend("topright", 
       legend = c("Classical", "Robust"), 
       col = c("blue", "red"), 
       lty = c(1, 2), 
       fill = c("blue", "red")
       )

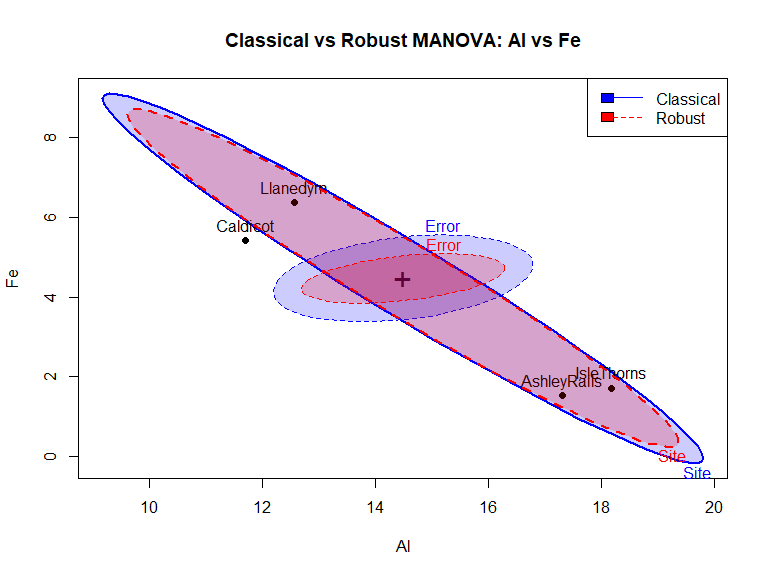
Figure 7: HE plot comparing classical (blue) and robust (red) MANOVA for Al vs Fe

The H and E ellipses have approximately the same shape and orientation for the classical and robust models, indicating that the pattern of differences among the group means is quite similar for both models. However, the E ellipse for the robust model is noticeably smaller. This goes into the greater $F$ statistic for the robust model.

For a more complete interpretation of robust model, a scatterplot matrix of HE plots is shown below, using the pairs() method for a MLM.

pairs(pottery.rlm, 
      fill=TRUE, fill.alpha = 0.1)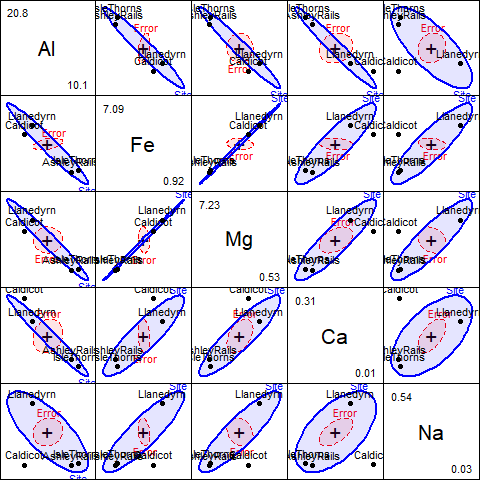

Figure 8: Pairwise HE plots for all response variables in the robust model pottery.rlm

Interpretation and Discussion

Several important insights emerge from this analysis of the Pottery data

• Model evaluation: The comparison of MANOVA results shows …

• Outlier detection: The weight plot identifies specific observations that deviate from the typical pattern. In archaeological studies, such outliers might represent pottery from different time periods, contaminated samples, or measurement errors that warrant further investigation.

• Geometric interpretation: The HE plot comparison reveals how outliers affect the geometric representation of the hypothesis test. The hypothesis ellipse (representing the Site effect) and error ellipse (representing within-group variation) may differ substantially between classical and robust fits when influential outliers are present. The usual effect is that of seeing hypothesis effects more strongly when potential outliers are down-weighted.

• Practical implications: For archaeologists studying historical artifacts, the robust analysis provides more reliable conclusions about site or other factors differences by reducing the influence of potentially problematic observations. This is particularly important when making inferences about ancient trade routes, cultural practices, or chronological relationships based on chemical composition data. In some circumstances, the identification of such unusual observations can lead to insight about conventional theory.

The robust approach demonstrates its value by providing a more stable analysis that is less susceptible to the influence of outlying observations, while still maintaining high efficiency when the data conform to standard assumptions.

Example: Pulp Fiber Data

Our second example is more compact, and illustrates robmlm() in a multivariate multiple regression rather than a MANOVA design. The pulpfiber data [in the robustbase package, Rousseeuw et al. (2004); data from the unpublished thesis of Lee, 1992] give four pulp-fiber properties (X1-X4: fiber length, long fiber fraction, fine fiber fraction, zero-span tensile) measured on 62 samples, along with four properties of the paper produced from them (Y1-Y4: breaking length, elastic modulus, failure stress, burst strength). The goal is to predict the paper properties from the fiber properties.

data(pulpfiber, package = "robustbase")
str(pulpfiber)
#> 'data.frame':    62 obs. of  8 variables:
#>  $ X1: num  -0.03 0.015 0.025 0.03 -0.07 -0.05 -0.247 -0.099 -0.242 -0.188 ...
#>  $ X2: num  35.2 35.7 39.2 39.8 33 ...
#>  $ X3: num  37 36.9 30.6 21.1 36.6 ...
#>  $ X4: num  1.06 1.06 1.05 1.05 1.05 ...
#>  $ Y1: num  21.3 21.2 20.7 19.5 20.4 ...
#>  $ Y2: num  7.04 6.98 6.78 6.6 6.79 ...
#>  $ Y3: num  5.33 5.24 5.06 4.48 4.91 ...
#>  $ Y4: num  0.932 0.871 0.742 0.513 0.577 0.784 0.358 0.215 0.432 0.372 ...

Classical and Robust Fits

To get started, fit the classical OLS multivariate regression and the robust version and run car::Anova() on each

pulp.mod <- lm(cbind(Y1, Y2, Y3, Y4) ~ X1 + X2 + X3 + X4, data = pulpfiber)
pulp.rlm <- robmlm(cbind(Y1, Y2, Y3, Y4) ~ X1 + X2 + X3 + X4, data = pulpfiber)

Anova(pulp.mod)
#> 
#> Type II MANOVA Tests: Pillai test statistic
#>    Df test stat approx F num Df den Df  Pr(>F)    
#> X1  1     0.157     2.51      4     54   0.053 .  
#> X2  1     0.404     9.16      4     54 1.0e-05 ***
#> X3  1     0.211     3.62      4     54   0.011 *  
#> X4  1     0.695    30.80      4     54 2.3e-13 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Anova(pulp.rlm)
#> 
#> Type II MANOVA Tests: Pillai test statistic
#>    Df test stat approx F num Df den Df  Pr(>F)    
#> X1  1     0.357      6.9      4     50 0.00016 ***
#> X2  1     0.534     14.3      4     50 7.2e-08 ***
#> X3  1     0.368      7.3      4     50 0.00011 ***
#> X4  1     0.764     40.4      4     50 4.4e-15 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The contrast here is more dramatic than for Pottery:

• In the classical fit, X2 and X4 stand out clearly ($p < .0001$), X3 is only marginally significant ($p = .011$), and X1 falls just short of conventional significance ($p = .053$).
• In the robust fit, by contrast, all four fiber properties are highly significant predictors of the paper properties ($p < .001$ in every case). This suggests that a handful of atypical samples in the classical fit are masking real predictive relationships involving X1 and X3.

Robust Weights

plot(pulp.rlm, segments = TRUE)

Figure 9: Weights from robust fitting of the pulp fiber data

Four cases – 51, 52, 56 and 61 – are driven to (essentially) zero weight; two more (22, 44) are markedly reduced (0.43 and 0.69); every other sample retains weight above 0.7. The weight plot alone doesn’t say why these six are atypical; for that we turn to the distance plot.

Distance Plot

A distancePlot() involves two independent choices: which residuals define the Y (vertical) axis – from pulp.mod (OLS) or pulp.rlm (robust) – and which covariance estimator computes the distances themselves, via method. In this example, only the second choice matters much: with the default method = "classical", the flagged cases are identical whether the residuals come from pulp.mod or pulp.rlm – the same eight cases (46, 51, 52, 56, 57, 58, 60, 61) either way. The main difference is seen in the covariance estimate, not the fit.

The reason is a masking effect: classical covariance for the X1-X4 fiber measurements is computed from all 62 samples, including the very outliers it is meant to help detect, so it is itself distorted by them and understates how unusual those samples really are. Rousseeuw et al. (2004) address exactly this for the pulp fiber data by using the MCD covariance estimator instead, which is resistant to the outliers it’s estimating around. The panels below compare the two, both using the robust-fit residuals from pulp.rlm:

op <- par(mfrow = c(1, 2))
distancePlot(pulp.rlm, method = "classical", main = "Classical distances")
#> 0.975 X, Y distance cutoffs: 3.338 3.338
distancePlot(pulp.rlm, method = "mcd", main = "MCD distances")
#> 0.975 X, Y distance cutoffs: 3.338 3.338

Figure 10: Distance plots for the robust pulp fiber model, comparing classical (left) and MCD-based (right) covariance estimates for the fiber (X) predictor distances.

par(op)

Under classical covariance (left), cases 60 and 62 – which turn out to have the two largest predictor distances of any sample once MCD is used – don’t stand out at all: their unusual fiber measurements are masked by a covariance matrix that treats them as ordinary. Under MCD (right), the picture sharpens considerably, flagging 21 cases rather than 8. Most of these retain weight above 0.8 in pulp.rlm – unusual in X, but well fit by the model – so we focus on the few that also matter for the robust fit:

• Cases 51, 52 and 56 have unremarkable fiber measurements (small distance on X) but very large residual distances: vertical outliers, poorly predicted by the fitted relationship regardless of their (ordinary) predictor values. These are exactly the three cases driven to zero weight above.

• Case 61 is extreme on both axes: a bad leverage point, unusual in its fiber properties and poorly fit by the model – correctly downweighted to zero along with the vertical outliers.

• Cases 60 and 62 have the two largest predictor distances of any sample, by a wide margin, yet small residual distances: good leverage points. They are unusual fiber samples, but ones the fitted relationship predicts well, so robmlm() correctly leaves them at near-full weight (0.98 each) rather than downweighting them.

• Case 22 sits in between, at weight 0.43: moderately unusual on both axes without being fully downweighted – a reminder that robmlm()’s weighting is continuous, not the all-or-nothing split the labels above suggest.

Multivariate Influence Plots

What we can learn from a distancePlot() can be compared to alternative displays that generalize the traditional influence plots of residuals vs. leverage, which are extended to the MLM case in the mvinfluence package.

influencePlot() for an "mlm" object draws a bubble plot, with circle areas proportional to a generalized Cook’s distance, using one of three types of axes. The default, type = "stres", plots (squared) Studentized residuals directly against the hat values (leverage). type = "LR" instead plots transformed residual and leverage components, R and L, chosen so that contours of constant Cook’s distance fall on diagonal lines – useful for seeing at a glance whether a case’s influence comes mainly from an unusual response, an unusual predictor pattern, or both.

influencePlot(pulp.mod, id.n = 5)

Figure 11: Default (type = 'stres') multivariate influence plot for the OLS pulp fiber model.

#>          H       Q  CookD       L       R
#> 46 0.24366 0.05983 0.1662 0.32216 0.07911
#> 51 0.06929 0.61222 0.4836 0.07445 0.65779
#> 52 0.10600 0.41406 0.5004 0.11857 0.46316
#> 56 0.12652 0.69124 0.9970 0.14485 0.79137
#> 57 0.20519 0.04397 0.1029 0.25817 0.05532
#> 58 0.21948 0.05280 0.1321 0.28119 0.06765
#> 59 0.18955 0.18764 0.4055 0.23389 0.23153
#> 60 0.49040 0.09928 0.5551 0.96231 0.19483
#> 61 0.41128 0.38188 1.7904 0.69859 0.64865

influencePlot(pulp.mod, id.n = 5, type = "LR")

Figure 12: type = 'LR' multivariate influence plot for the same model.

#>          H       Q  CookD       L       R
#> 46 0.24366 0.05983 0.1662 0.32216 0.07911
#> 51 0.06929 0.61222 0.4836 0.07445 0.65779
#> 52 0.10600 0.41406 0.5004 0.11857 0.46316
#> 56 0.12652 0.69124 0.9970 0.14485 0.79137
#> 57 0.20519 0.04397 0.1029 0.25817 0.05532
#> 58 0.21948 0.05280 0.1321 0.28119 0.06765
#> 59 0.18955 0.18764 0.4055 0.23389 0.23153
#> 60 0.49040 0.09928 0.5551 0.96231 0.19483
#> 61 0.41128 0.38188 1.7904 0.69859 0.64865

Both types flag the same nine cases here (46, 51, 52, 56, 57, 58, 59, 60, 61) – switching type reorganizes how the same influence information is displayed, not which cases stand out. Case 61 has the largest bubble in both (generalized Cook’s D = 1.79), consistent with its bad-leverage status above, and case 60 has by far the largest leverage component L, consistent with it being the more extreme of the two good-leverage cases. Case 62, though, doesn’t appear here at all: influencePlot() uses the ordinary (non-robust) hat values from pulp.mod, under which case 62’s leverage ranks only 11th of 62 – the same classical-covariance masking that hid it from the distance plot above.

Interpretation and Discussion

• Model evaluation: The gain from 2 to 4 significant predictors under the robust fit shows how a small number of outlying samples can mask genuine predictive relationships in classical multivariate regression – a stronger contrast than in the Pottery example.

• Outlier detection: The weight plot and distance plot together tell a more nuanced story than “outlier” vs. “not”: some flagged cases (51, 52, 56, 61) are poorly fit and rightly downweighted, while others (60, 62) are merely unusual in their predictors and rightly are not. Distinguishing good from bad leverage points this way is exactly the diagnostic problem distancePlot() is designed to address.

• Practical implications: For process data like this – where fiber properties are measured to predict paper quality – correctly identifying which atypical samples to downweight (vertical/bad-leverage cases) versus keep (good-leverage cases) matters for building a model that generalizes to new, unusual-but-plausible fiber batches, rather than one that has simply been fit to accommodate a few mismeasured samples.

References

Huber, P. J. (1964). Robust estimation of a location parameter. The Annals of Mathematical Statistics, 35(1), 73–101.

Rousseeuw, P. J., Van Aelst, S., Van Driessen, K., & Gulló, J. A. (2004). Robust multivariate regression. Technometrics, 46(3), 293–305. http://doi.org/10.1198/004017004000000329

Rousseeuw, P. J., & Yohai, V. J. (1984). Robust regression by means of S-estimators. In J. Franke, W. Härdle, & D. Martin (Eds.), Robust and nonlinear time series analysis (Vol. 26, pp. 256–272). New York: Springer.

Rousseeuw, P. J., & Zomeren, B. C. van. (1990). Unmasking multivariate outliers and leverage points. Journal of the American Statistical Association, 85(411), 633–639. http://doi.org/10.1080/01621459.1990.10474920

Rousseeuw, P. J., & Zomeren, B. C. van. (1991). Robust distances: Simulation and cutoff values. In W. Stahel & S. Weisberg (Eds.), Directions in robust statistics and diagnostics, part II. New York: Springer-Verlag.

Tukey, J. W. (1960). A survey of sampling from contaminated distributions.

Yohai, V. J. (1987). High breakdown-point and high efficiency robust estimates for regression. The Annals of Statistics, 15(2), 642–656.