Variance Inflation Factors for Ridge Regression

The function vif.ridge calculates variance inflation factors for the predictors in a set of ridge regression models indexed by the tuning/shrinkage factor, returning one row for each value of the \(\lambda\) parameter.

Variance inflation factors are calculated using the simplified formulation in Fox & Monette (1992).

The plot.vif.ridge method plots variance inflation factors for a "vif.ridge" object in a similar style to what is provided by traceplot. That is, it plots the VIF for each coefficient in the model against either the ridge \(\lambda\) tuning constant or it's equivalent effective degrees of freedom.

Usage

# S3 method for class 'ridge'
vif(mod, ...)

# S3 method for class 'vif.ridge'
print(x, digits = max(4, getOption("digits") - 5), ...)

# S3 method for class 'vif.ridge'
plot(
  x,
  X = c("lambda", "df"),
  col = c("black", "red", "darkgreen", "blue", "darkcyan", "magenta", "brown",
    "darkgray"),
  pch = c(15:18, 7, 9, 12, 13),
  xlab,
  ylab = "Variance Inflation",
  xlim,
  ylim,
  ...
)

Arguments

mod: A "ridge" object computed by ridge
...: Other arguments passed to methods
x: A ridge object, as fit by ridge
digits: Number of digits to display in the print method
X: What to plot as the horizontal coordinate, one of c("lambda", "df")
col: A numeric or character vector giving the colors used to plot the ridge trace curves. Recycled as necessary.
pch: Vector of plotting characters used to plot the ridge trace curves. Recycled as necessary.
xlab: Label for horizontal axis
ylab: Label for vertical axis
xlim, ylim: x, y limits for the plot. You may need to adjust these to allow for the variable labels.

Value

vif returns a "vif.ridge" object, which is a list of four components

vif: a data frame of the same size and shape as coef{mod}. The columns correspond to the predictors in the model and the rows correspond to the values of lambda in ridge estimation.
lambda: the vector of ridge constants from the original call to ridge
df: the vector of effective degrees of freedom corresponding to lambda
criteria: the optimal values of lambda

References

Fox, J. and Monette, G. (1992). Generalized collinearity diagnostics. JASA, 87, 178-183, doi:10.1080/01621459.1992.10475190 .

Author

Michael Friendly

Examples


data(longley)
lmod <- lm(Employed ~ GNP + Unemployed + Armed.Forces + Population + 
                      Year + GNP.deflator, data=longley)
vif(lmod)
#>          GNP   Unemployed Armed.Forces   Population         Year GNP.deflator 
#>   1788.51348     33.61889      3.58893    399.15102    758.98060    135.53244 

lambda <- c(0, 0.005, 0.01, 0.02, 0.04, 0.08)
lridge <- ridge(Employed ~ GNP + Unemployed + Armed.Forces + 
                           Population + Year + GNP.deflator, 
                 data=longley, lambda=lambda)

coef(lridge)
#>              GNP Unemployed Armed.Forces  Population     Year GNP.deflator
#> 0.000 -3.4471925  -1.827886   -0.6962102 -0.34419721 8.431972   0.15737965
#> 0.005 -1.0424783  -1.491395   -0.6234680 -0.93558040 6.566532  -0.04175039
#> 0.010 -0.1797967  -1.361047   -0.5881396 -1.00316772 5.656287  -0.02612152
#> 0.020  0.4994945  -1.245137   -0.5476331 -0.86755299 4.626116   0.09766305
#> 0.040  0.9059471  -1.155229   -0.5039108 -0.52347060 3.576502   0.32123994
#> 0.080  1.0907048  -1.086421   -0.4582525 -0.08596324 2.641649   0.57025165

# get VIFs for the shrunk estimates
vridge <- vif(lridge)
vridge
#> Variance inflaction factors:
#>            GNP  Unemployed  Armed.Forces  Population    Year  GNP.deflator
#> 0.000  1788.51      33.619         3.589      399.15  758.98        135.53
#> 0.005   540.04      12.118         2.921      193.30  336.15         90.63
#> 0.010   259.00       7.284         2.733      134.42  218.84         74.79
#> 0.020   101.12       4.573         2.578       87.29  128.82         58.94
#> 0.040    34.43       3.422         2.441       52.22   66.31         43.56
#> 0.080    11.28       2.994         2.301       28.59   28.82         29.52

# plot VIFs
pch <- c(15:18, 7, 9)
clr <- c("black", rainbow(5, start=.6, end=.1))

### Transition examples, because the vif() method now returns a list structure 
### rather than a data.frame 
vr <- vridge$vif
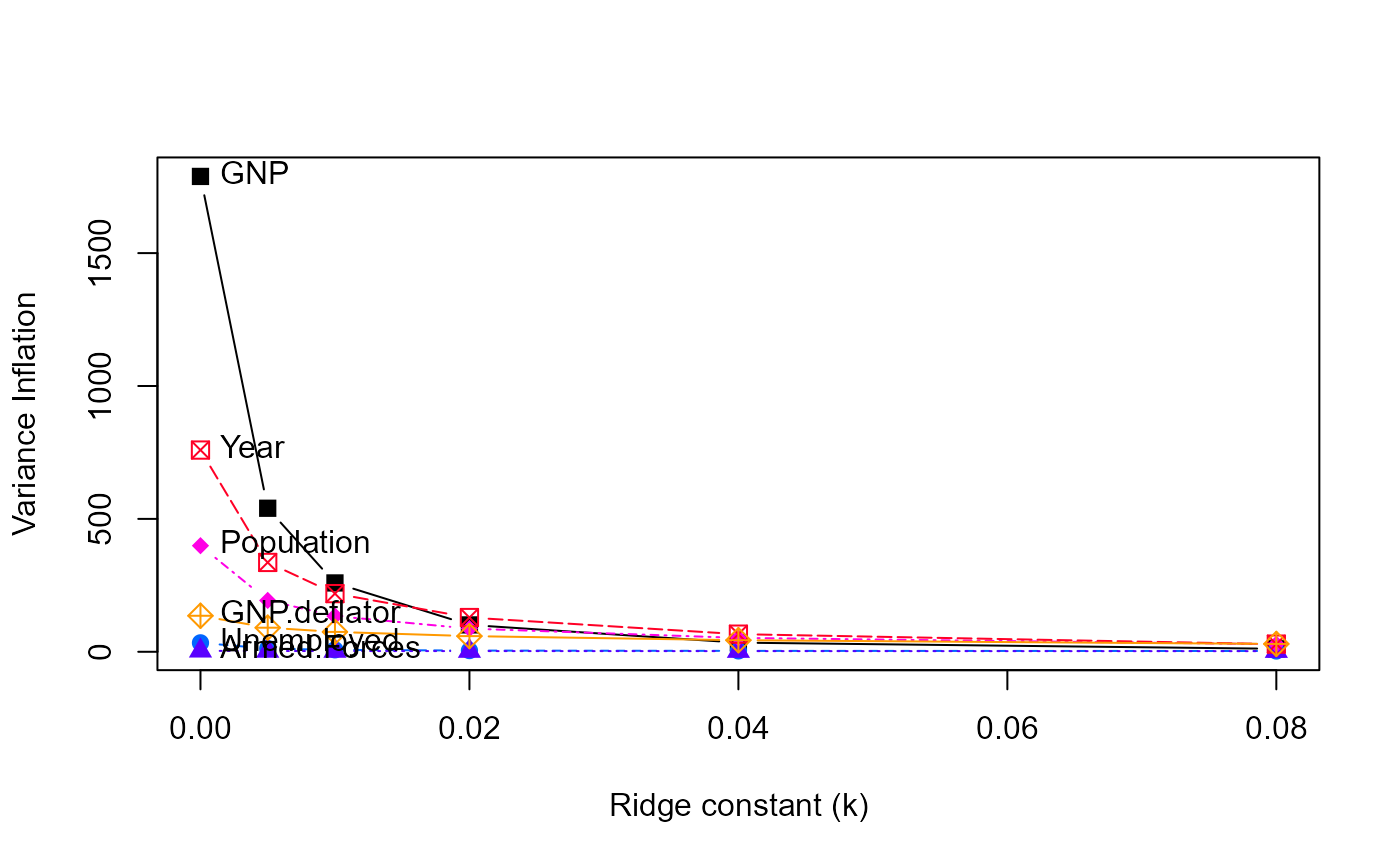
matplot(rownames(vr), vr, type='b', 
  xlab='Ridge constant (k)', ylab="Variance Inflation", 
  xlim=c(0, 0.08), 
  col=clr, pch=pch, cex=1.2)
text(0.0, vr[1,], colnames(vr), pos=4)


# matplot(lridge$df, vridge, type='b', 
#   xlab='Degrees of freedom', ylab="Variance Inflation", 
#  col=clr, pch=pch, cex=1.2)
# text(6, vridge[1,], colnames(vridge), pos=2)

# more useful to plot VIF on the sqrt scale

# matplot(rownames(vridge), sqrt(vridge), type='b', 
#  xlab='Ridge constant (k)', ylab=expression(sqrt(VIF)), 
#  xlim=c(-0.01, 0.08), 
#  col=clr, pch=pch, cex=1.2, cex.lab=1.25)
# text(-0.01, sqrt(vridge[1,]), colnames(vridge), pos=4, cex=1.2)

# matplot(lridge$df, sqrt(vridge), type='b', 
#  xlab='Degrees of freedom', ylab=expression(sqrt(VIF)), 
#  col=clr, pch=pch, cex=1.2, cex.lab=1.25)
# text(6, sqrt(vridge[1,]), colnames(vridge), pos=2, cex=1.2)