Plotting nestedLogit models with ggplot2

Load the packages we’ll use here:

library(nestedLogit)    # Nested Dichotomy Logistic Regression Models
library(knitr)          # A General-Purpose Package for Dynamic Report Generation in R
library(dplyr)          # A Grammar of Data Manipulation
library(tidyr)          # Tidy Messy Data
library(ggplot2)        # Create Elegant Data Visualisations Using the Grammar of Graphics
library(geomtextpath)   # Curved Text in 'ggplot2'

The main vignette illustrated the basic plot method, plot.nestedLogit() in the package. However, for better control of the details and possibly more pleasing graphs, it is useful to describe how graphs can be constructed using ggplot2 (Wickham et al., 2023). We’ll use the same example of women’s labor force participation, using the original dichotomies:

data(Womenlf, package = "carData")
comparisons <- logits(work=dichotomy("not.work", c("parttime", "fulltime")),
                      full=dichotomy("parttime", "fulltime"))

wlf.nested <- nestedLogit(partic ~ hincome + children,
                          dichotomies = comparisons,
                          data=Womenlf)

The advantages of this approach are that

you can handle more complicated designs with more predictors by faceting,
it allows you to plot either the fitted probabilities or their transformed logits,
you can also obtain plots for log odds corresponding to each of the dichotomies which comprise the nested logit model.

As we will illustrate, this provides a nice visual interpretation of the alternative specification of dichotomies for the Womenlf data discussed in the section “Alternative models for the Womenlf data” of the main vignette.

Fitted probabilities

To draw a plot, it is sufficient to calculate predicted probabilities over a grid of values of the predictor variables. Here, we select a range of 0 - 45 in steps of 5, combined with the two values of children.

new <- expand.grid(hincome=seq(0, 45, by = 5),
                   children=c("absent", "present"))

pred.nested <- predict(wlf.nested, newdata = new)
names(pred.nested)
#> [1] "p"        "logit"    "se.p"     "se.logit" ".data"

As explained in help(predict.nestedLogit), the predict method returns a complicated structure – a list of four data frames corresponding to the predicted probabilities for the response categories, the corresponding logits, and each of their standard errors.

head(pred.nested[["p"]])
#>   not.work parttime fulltime
#> 1   0.2082  0.02372   0.7681
#> 2   0.2452  0.03785   0.7169
#> 3   0.2864  0.05907   0.6545
#> 4   0.3315  0.08936   0.5791
#> 5   0.3800  0.12944   0.4906
#> 6   0.4309  0.17691   0.3922

However, ggplot wants the data in long format. This is easily done using the as.data.frame() method, which also includes the values of the predictors in the newdata data set:

plotdata <- as.data.frame(pred.nested, newdata=new)
head(plotdata)
#>   hincome children response       p    se.p   logit se.logit
#> 1       0   absent not.work 0.20820 0.06326 -1.3358   0.3838
#> 2       0   absent parttime 0.02372 0.01775 -3.7176   0.7666
#> 3       0   absent fulltime 0.76809 0.06386  1.1975   0.3585
#> 4       5   absent not.work 0.24522 0.05799 -1.1243   0.3133
#> 5       5   absent parttime 0.03785 0.02222 -3.2356   0.6101
#> 6       5   absent fulltime 0.71694 0.05933  0.9293   0.2923

Plotting with `ggplot2`

Then we can plot probability against one predictor, use color to distinguish the levels of the response (partic) and facet the plot by children. The point-wise standard errors are drawn in a 68% confidence envelope using geom_ribbon(). We’ve also plotted the predicted values as points to show where the predictions are obtained.

theme_set(theme_bw(base_size = 14))

gg1 <- ggplot(plotdata,
       aes(x=hincome, y=p, color=response)) +
  geom_line(linewidth = 2) +
  geom_point(size = 1.5, shape = 16, color = "black") +
  labs(x="Husband's Income", y= "Probability") +
  facet_wrap(~ children, labeller = label_both) +
  geom_ribbon(aes(ymin=p - se.p,
                  ymax=p + se.p,
                  fill = response), alpha = 0.3) 

gg1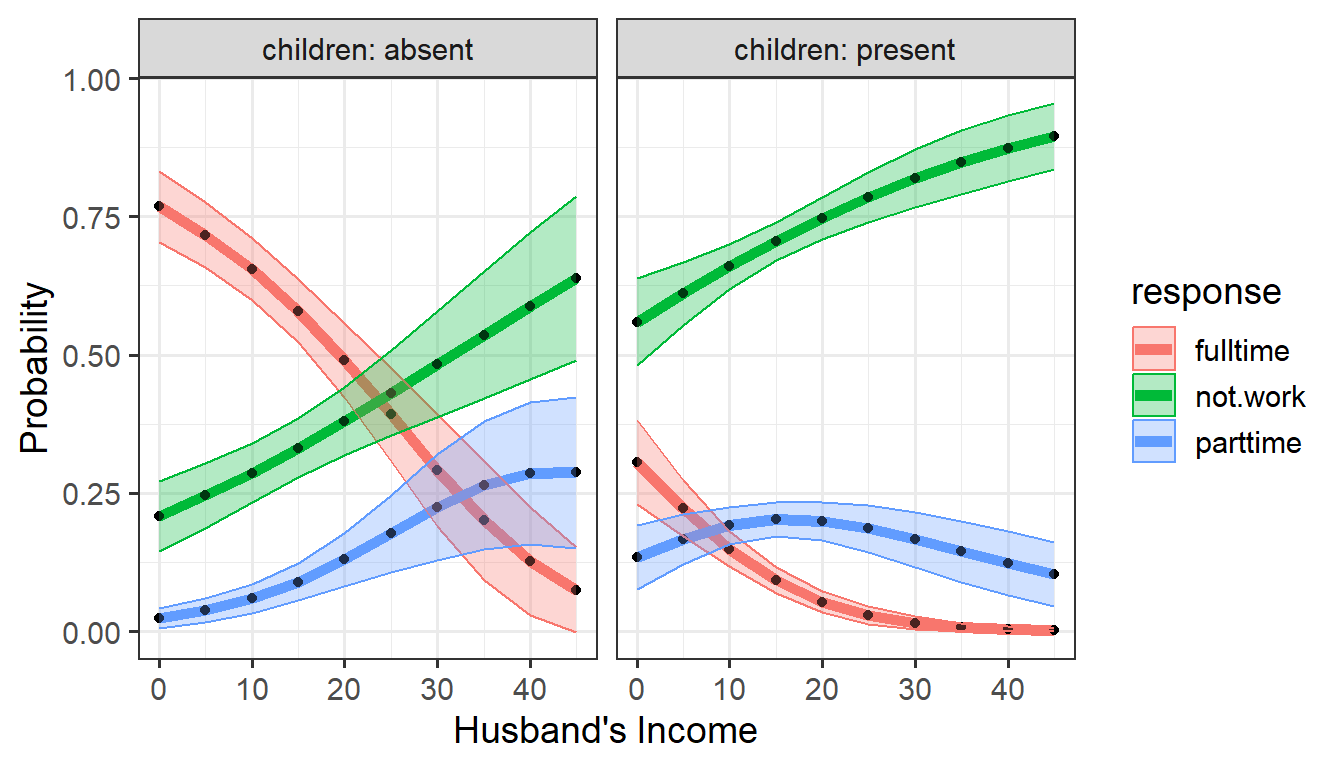

ggplot: Predicted probabilities of working at all or working part time or full time versus husband’s income, by children

It is noteworthy that the confidence envelopes are wider for not-working women at higher levels of husband’s income, where there are fewer observations.

Direct labels

Plot legends are somewhat hard to read and take up unnecessary space in the plot, so it is often better to label the curves directly. The geomtextpath package (Cameron & van den Brand, 2022) produces a nicer plot.

gg1 + geom_textline(aes(label = response), 
                    hjust = -0.01, vjust=-0.5, size=5) +
  theme(legend.position = "none")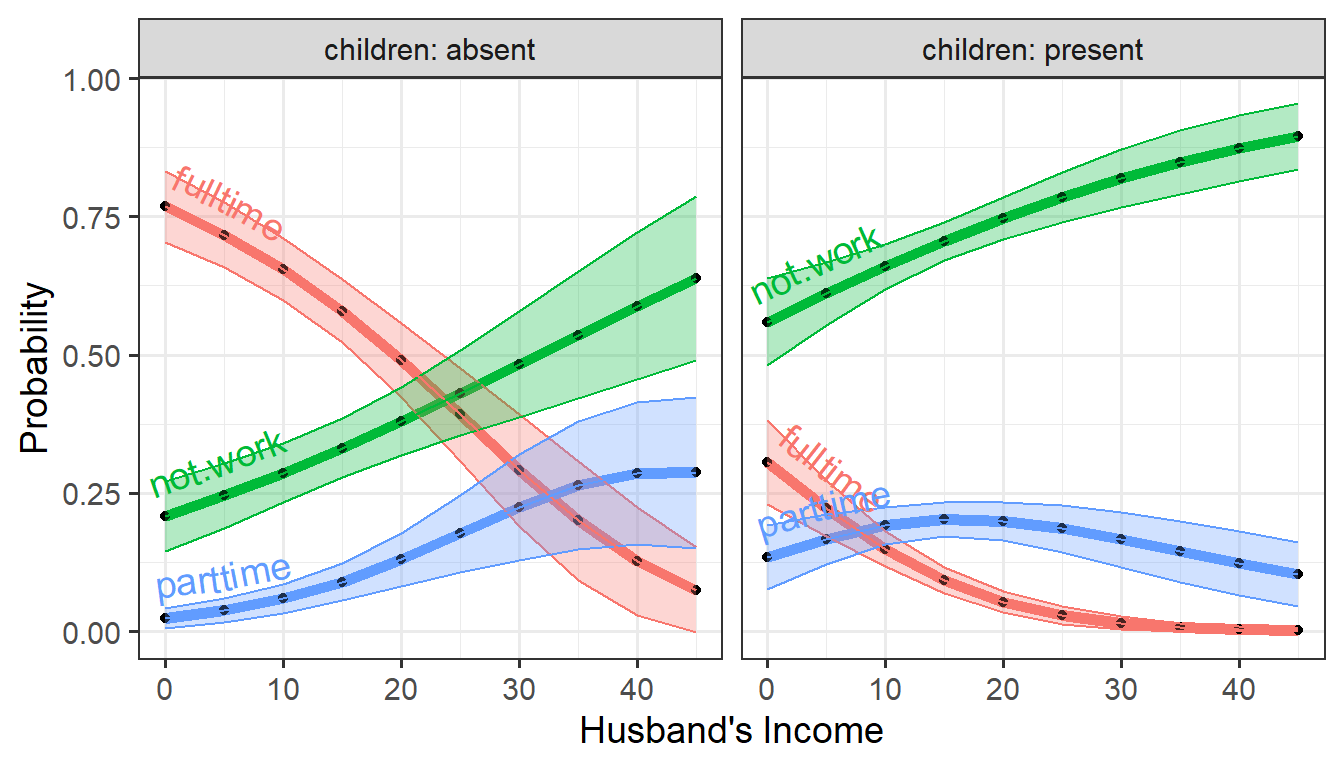

The same plot using direct labels on the curves rather than a legend.`

Plotting log-odds

The advantage of the data structure returned by as.data.frame() is that you can just as easily plot the predicted probabilities on the scale of log-odds (\(\text{logit}(p) = \log(p / (1-p))\)), using the logit and logit.se components.

ggplot(plotdata,
       aes(x=hincome, y=logit, color=response)) +
  geom_line(linewidth = 2) +
  geom_point(size = 1.5, shape = 16, color = "black") +
  labs(x="Husband's Income", y= "Log Odds") +
  facet_wrap(~ children, labeller = label_both) +
  geom_ribbon(aes(ymin=logit - se.logit,
                  ymax=logit + se.logit,
                  fill = response), alpha = 0.3) +
  geom_textline(aes(label = response), 
                hjust = -0.01, vjust=-0.5, size=5) +
  theme(legend.position = "none")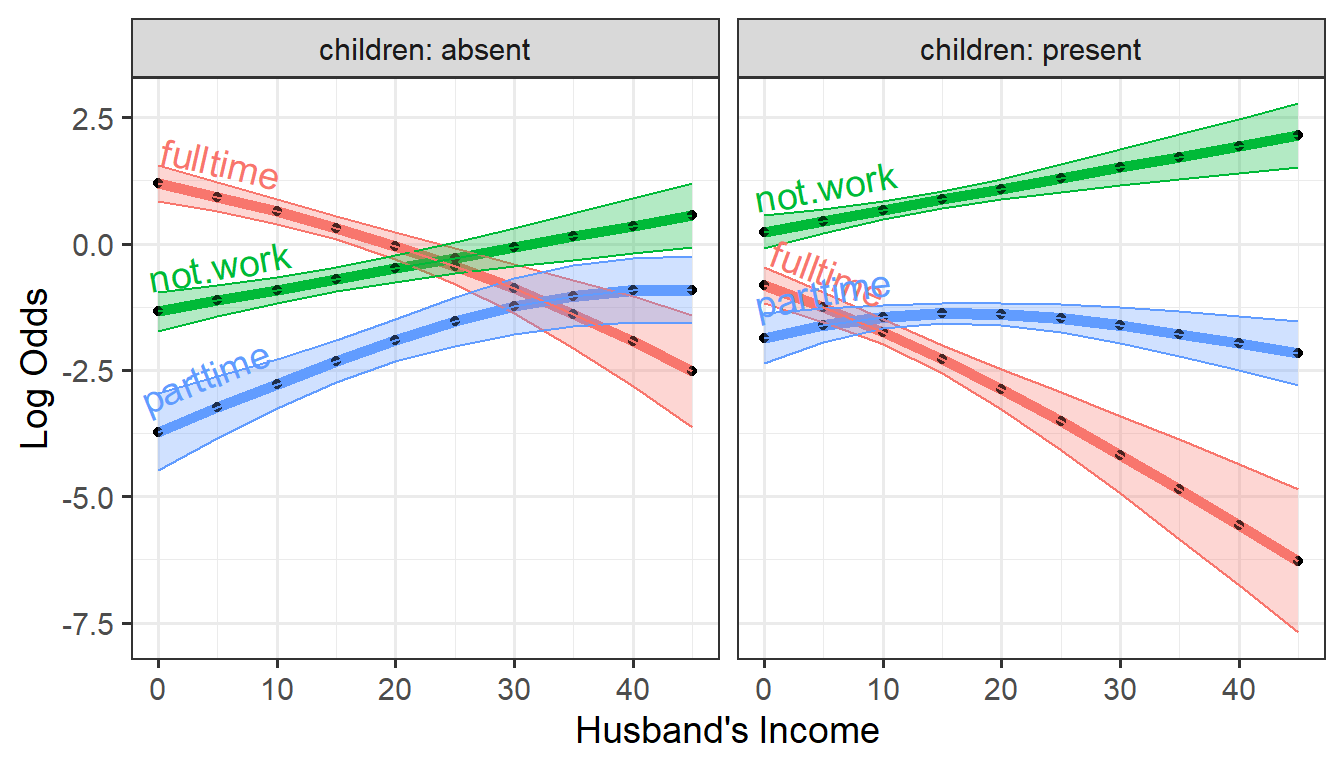

Predicted log odds of working at all or working part time or full time versus husband’s income, by children

Predicted logit values for the dichotomies

The nested logit model wlf.nested comprises the two binary logistic regression models for the work and full dichotomies. We can plot these as follows.

names(models(wlf.nested))
#> [1] "work" "full"

The predict() method can also generate predicted values and their standard errors for the logits of these dichotomies, using the model = "dichotomies" argument:

pred.dichot <- predict(wlf.nested, newdata = new,
                       model = "dichotomies")
str(pred.dichot)
#> List of 3
#>  $ work :'data.frame':   20 obs. of  3 variables:
#>   ..$ fit           : num [1:20] 1.336 1.124 0.913 0.701 0.49 ...
#>   ..$ se.fit        : num [1:20] 0.384 0.313 0.262 0.242 0.261 ...
#>   ..$ residual.scale: num [1:20] 1 1 1 1 1 1 1 1 1 1 ...
#>  $ full :'data.frame':   20 obs. of  3 variables:
#>   ..$ fit           : num [1:20] 3.48 2.94 2.41 1.87 1.33 ...
#>   ..$ se.fit        : num [1:20] 0.767 0.613 0.489 0.423 0.443 ...
#>   ..$ residual.scale: num [1:20] 1 1 1 1 1 1 1 1 1 1 ...
#>  $ .data:'data.frame':   20 obs. of  2 variables:
#>   ..$ hincome : num [1:20] 0 5 10 15 20 25 30 35 40 45 ...
#>   ..$ children: Factor w/ 2 levels "absent","present": 1 1 1 1 1 1 1 1 1 1 ...
#>   ..- attr(*, "out.attrs")=List of 2
#>   .. ..$ dim     : Named int [1:2] 10 2
#>   .. .. ..- attr(*, "names")= chr [1:2] "hincome" "children"
#>   .. ..$ dimnames:List of 2
#>   .. .. ..$ hincome : chr [1:10] "hincome= 0" "hincome= 5" "hincome=10" "hincome=15" ...
#>   .. .. ..$ children: chr [1:2] "children=absent" "children=present"
#>  - attr(*, "model")= chr "wlf.nested"
#>  - attr(*, "dichotomies")= chr [1:2] "work" "full"
#>  - attr(*, "class")= chr "predictDichotomies"

Transforming this to a data frame, we get an analogous result for plotting:

plotlogit <- as.data.frame(pred.dichot, newdata = new)
head(plotlogit)
#>   hincome children response  logit se.logit
#> 1       0   absent     work 1.3358   0.3838
#> 2       5   absent     work 1.1243   0.3133
#> 3      10   absent     work 0.9127   0.2620
#> 4      15   absent     work 0.7012   0.2422
#> 5      20   absent     work 0.4897   0.2613
#> 6      25   absent     work 0.2781   0.3121

Then, plot the logit vs. husband’s income, with separate curves for the two sub-models:

ggplot(plotlogit,
       aes(x=hincome, y=logit, color=response)) +
  geom_line(linewidth = 2) +
  geom_point(size = 1.5, shape = 16, color = "black") +
  labs(x="Husband's Income", y= "Log Odds") +
  facet_wrap(~ children, labeller = label_both) +
  geom_ribbon(aes(ymin=logit - se.logit,
                  ymax=logit + se.logit,
                  fill = response), alpha = 0.3) +
  geom_textline(aes(label = response),
                hjust = -0.01, vjust=-0.5, size=5) +
  theme(legend.position = "none")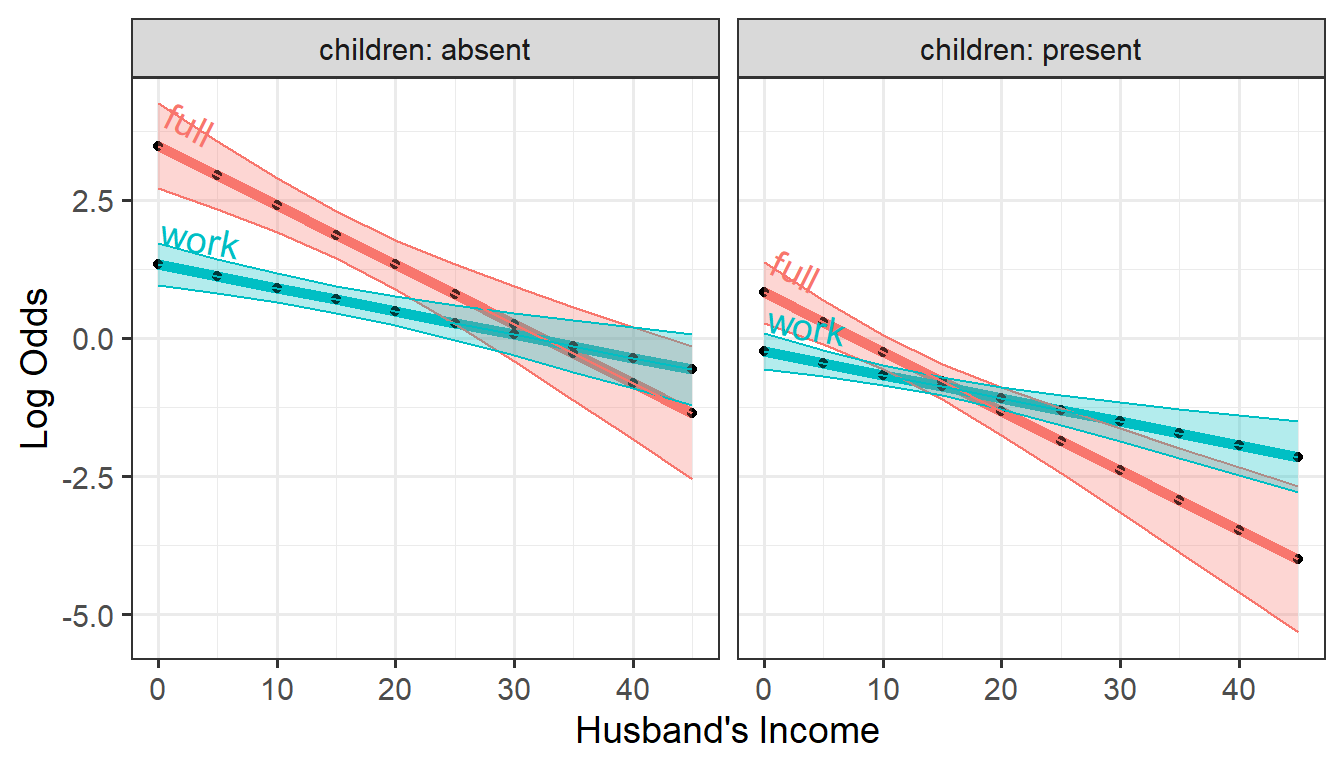

Predicted logits for the two dichotomies, work and full versus hincome, by children

Or, interchanging the roles of children and response, we can plot these the other way, faceting by response.

ggplot(plotlogit,
       aes(x=hincome, y=logit, color=children)) +
  geom_line(linewidth = 2) +
  geom_point(size = 1.5, shape = 16, color = "black") +
  labs(x="Husband's Income", y= "Log Odds") +
  facet_wrap(~ response, labeller = label_both) +
  geom_ribbon(aes(ymin=logit - se.logit,
                  ymax=logit + se.logit,
                  fill = children), alpha = 0.3) +
  geom_textline(aes(label = children),
                hjust = -0.01, vjust=-0.5, size=5) +
  theme(legend.position = "none")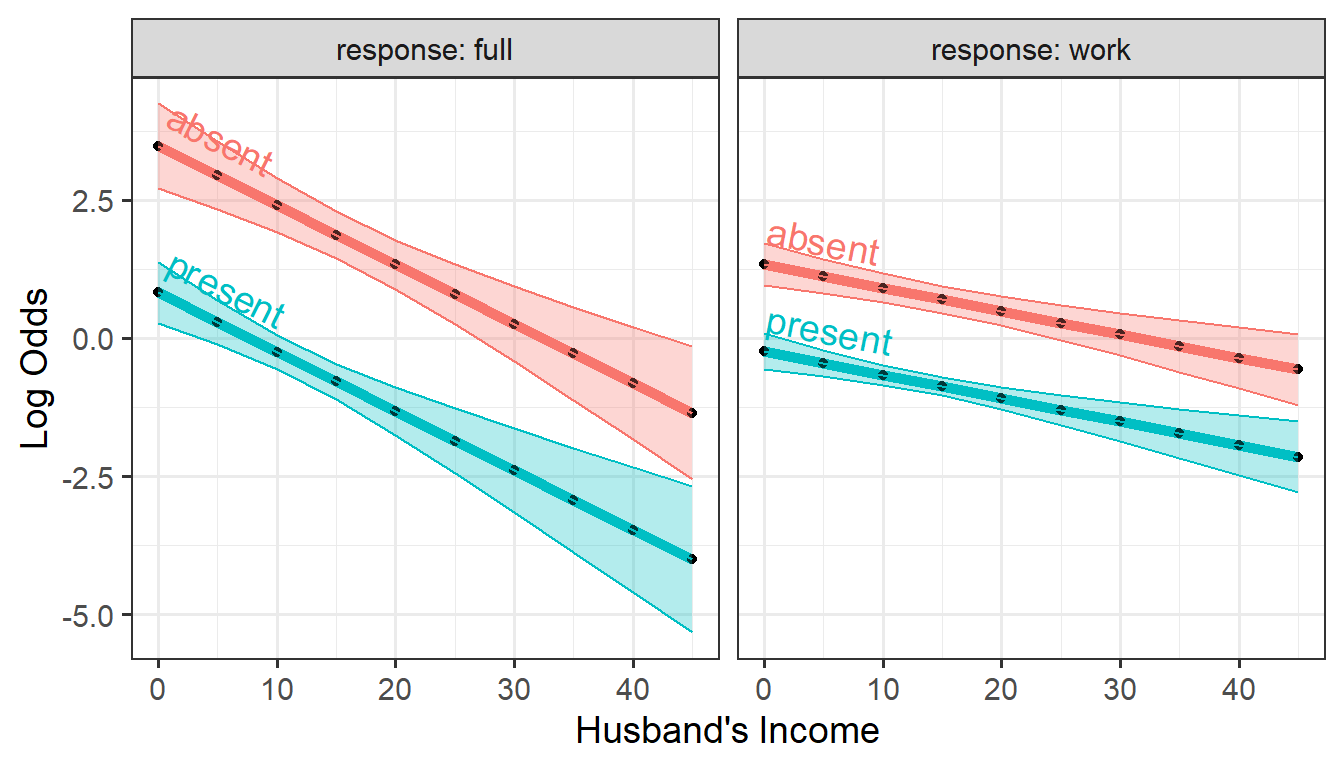

Predicted logits for the two dichotomies, work and full versus hincome, by response

This nicely illustrates the nature of the fitted logit models: The lines in each panel have the same slopes for the two levels of children, differing only in their intercepts. The full distinction between working full-time vs. part-time decreases faster with husband’s income than for the work dichotomy between not working at all and working either part-time or full-time.

Alternative model

In the main vignette we mentioned that an alternative set of nested dichotomies first contrasts full-time work with the other categories, {full-time} vs. {not working, part-time}, and then {not working} vs. {part-time}.

wlf.nested.alt <- nestedLogit(partic ~ hincome + children,
                              logits(full=dichotomy(nonfulltime=c("not.work", "parttime"), "fulltime"),
                                     part=dichotomy("not.work", "parttime")),
                              data=Womenlf)

Proceeding in the same way as above, we get predicted logits and standard errors for each of the dichotomies.

pred.dichot.alt <- predict(wlf.nested.alt, newdata = new,
                       model = "dichotomies")
plotlogit.alt <- as.data.frame(pred.dichot.alt, newdata = new)
head(plotlogit.alt)
#>   hincome children response   logit se.logit
#> 1       0   absent     full  1.7696   0.4690
#> 2       5   absent     full  1.2762   0.3577
#> 3      10   absent     full  0.7827   0.2723
#> 4      15   absent     full  0.2893   0.2421
#> 5      20   absent     full -0.2042   0.2852
#> 6      25   absent     full -0.6976   0.3772

Plotting these as before:

ggplot(plotlogit.alt,
       aes(x=hincome, y=logit, color=children)) +
  geom_line(linewidth = 2) +
  geom_point(size = 1.5, shape = 16, color = "black") +
  labs(x="Husband's Income", y= "Log Odds") +
  facet_wrap(~ response, labeller = label_both) +
  geom_ribbon(aes(ymin=logit - se.logit,
                  ymax=logit + se.logit,
                  fill = children), alpha = 0.3) +
  geom_textline(aes(label = children),
                hjust = -0.01, vjust=-0.5, size=5) +
  theme(legend.position = "none")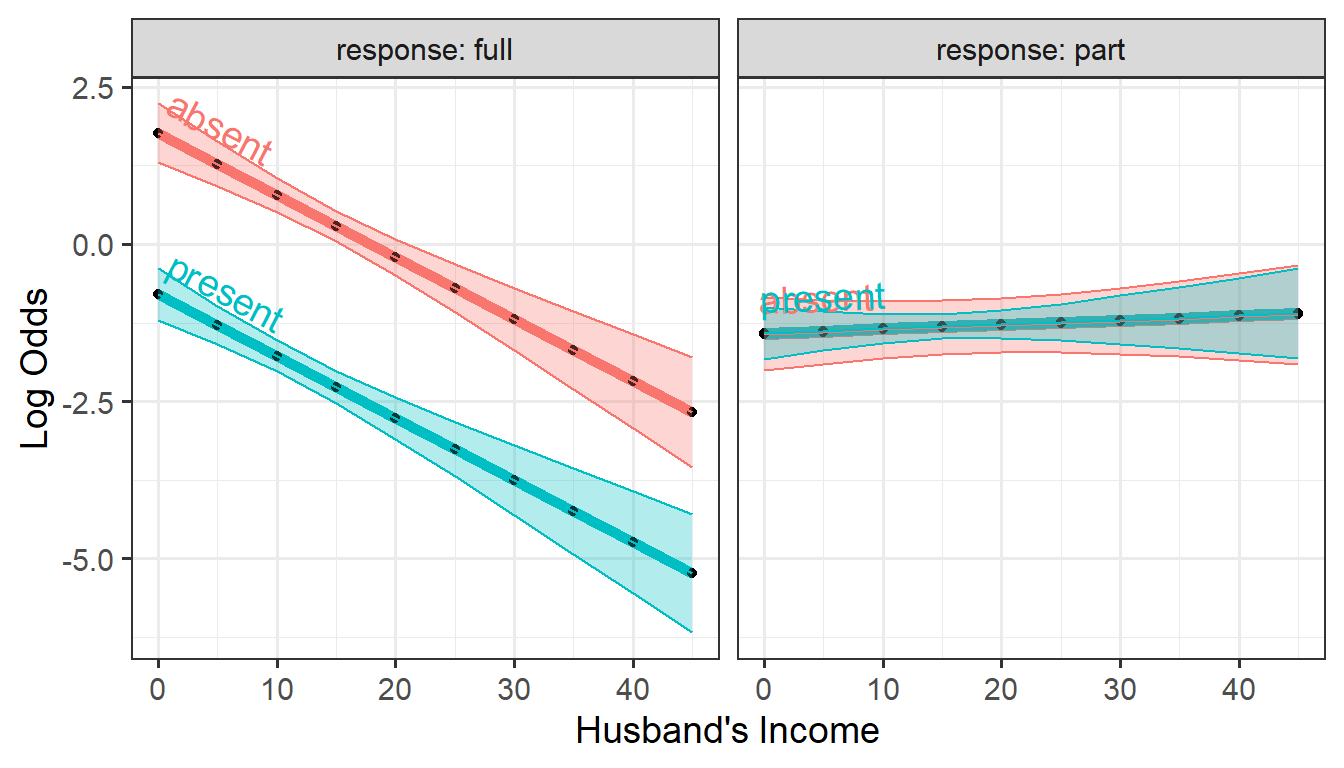

Predicted logits for the two dichotomies, work and full versus hincome, by response

It’s apparent that the alternative model produces a simpler description of the data: The predictors husband’s income and presence of children affect the decision to work full-time, but not the decision to work part-time among those who aren’t engaged in full-time work. In particular it is clear that neither husband’s income nor having young children has any effect on the decision to work part-time.

References

Cameron, A., & van den Brand, T. (2022). Geomtextpath: Curved text in ggplot2. Retrieved from https://allancameron.github.io/geomtextpath/

Wickham, H., Chang, W., Henry, L., Pedersen, T. L., Takahashi, K., Wilke, C., … Dunnington, D. (2023). ggplot2: Create elegant data visualisations using the grammar of graphics. Retrieved from https://CRAN.R-project.org/package=ggplot2

Michael Friendly and John Fox

2023-08-05

Fitted probabilities

Plotting with `ggplot2`

Direct labels

Plotting log-odds

Predicted logit values for the dichotomies

Alternative model

References

Plotting nestedLogit models with ggplot2

Michael Friendly and John Fox

2023-08-05

Fitted probabilities

Plotting with ggplot2

Direct labels

Plotting log-odds

Predicted logit values for the dichotomies

Alternative model

References

Plotting with `ggplot2`